The resuspension chamber as a tool for complex characterization of the quartz test aerosol
Resuspenzní komora jako nástroj ke komplexní charakterizaci křemenného aerosolového prachu
Martin Civiš 1,2
1Institute for Environmental Studies, Faculty of Science, Charles University in Prague, Benátská 2, 128 01 Prague 2, Czech Republic, civis@email.cz
2Institute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 2, 182 21 Prague 8, Czech Republic, civis@email.cz
Abstract
A quartz test powder aerosol was dispersed in a cylindrical resuspension chamber (V=0.437 m3, S=0.35 m2, S/V=8.38) and the temporal variation of size distribution was viewed on-line by an APS (Aerodynamic Particle Sizer) analyzer under the conditions of a controlled temperature of 20°C and a relative humidity (RH) of 50 %. The optimal mass load of the powder (with the highest mass concentrations after suspension) was 10 mg. The total number of 300 size distributions was used to calculate the average number and mass size distribution. The number or mass median particle diameter was 1.07 μm or 2.42 μm respectively. the median particle diameters were later used as input parameters into the mathematical models of project SPREAD. Deposition velocities of the particles suspended in the chamber were studied under the conditions of ventilators on and ventilators off. The calculated deposition velocity obtained with switched off ventilators was compared to the model of terminal settling velocity. The results were within 10 % agreement. The particle median diameters were inputted together with the surface parameters used in project SPREAD in the Raupach model and the change of deposition velocity with increasing wind speed was evaluated. It was found that increasing wind velocity and obstacles have the highest influence on the deposition velocity of particles of this size.
Keywords: resuspension chamber, APS, settling velocity, Stokes number
Abstrakt
Částice křemenného aerosolového prachu byly dispergovány a on-line sledovány pomocí APS (Aerodynamic Particle Sizer) v cylindrické resuspenzní komoře (V=0.437 m3, S=0.35 m2, S/V=8.38) za kontrolovaných podmínek teploty (20 ^(o)C) a relativní vlhkosti (50 %). Byla stanovena optimální navážka vzorku (umožňující maximální hmotnostní koncentraci aerosolu po suspenzi)- 10 mg. Z 300 velikostních distribucí byla spočítány průměrné velikostní distribuce počtu a hmoty křemenných částic. Průměrná velikost částice ve velikostní distribuci počtu byla 1.07 ?m a 2.42 μm u velikostní distribuce hmoty. Statistické hodnoty velikostních průměrné velikostní distribuce počtu a hmoty částic byly použity jako vstupní parametry do matematických modelů projektu SPREAD. U částic jednotlivých velikostí byly studovány depoziční rychlosti za podmínek vypnutých a zapnutých ventilátorů. Depoziční rychlosti vypočítané za podmínek vypnutých ventilátorů byly porovnány s modelem konečné usazovací rychlosti. Obě rychlosti se od sebe nelišily víc jak o 10 %. Průměrná velikost částic z velikostní distribuce počtu částic a parametry povrchu při disperzi částic řízenou explozí během projektu SPREAD byly vloženy do Raupachova modelu k vypočítaní depoziční rychlosti částic se svyšující se rychlostí větru. Bylo zjištěno, že při zvyšující se rychlosti větru dochází u částic této velikosti ke snižování depoziční rychlosti.
Klíčová slova: resuspenzní komora, APS, depoziční rychlost, Stokesovo číslo
1. Introduction
The resuspension chamber is a very useful tool for the suspension and collection of aerosol particulates in a controlled laboratory environment. The obtained data are used for the determination of the particulate suspendability, physical characteristics and chemical composition. All this information is needed in order to estimate the toxicological risks connected to the emission of such particulates into the atmosphere from different source materials, natural and industrial accidents and terrorist attacks. The physical and chemical parameters from such studies are being used in models which evaluate the toxicological risks of emission and dispersion of such particulates under various different circumstances.
During the twentieth century, many works described devices for the production or resuspension of dust. These devices were designed for various purposes, for example: for the simulation of the contaminated air inside a dusty factory hall (Dahman et al., 1997); the control of industrial processes (ASTM, 1984); in the pharmaceutical industry for the development of dry inhalers which maximize the concentration of fine aerosol in order to achieve the longest possible path for the particles inside the respiratory tract after their inhalation (Hindle et al., 1996; Concessio et al., 1997; Newman and Buse, 2002; Newman, 2004); for the exposure of laboratory animals to high concentrations of mineral aerosols in studies of respiratory diseases (Muhle et al., 1990); for the preparation of samples for chemical analyses (Morales et al., 1994); for the measurement of the ecophysiological effect of dust on leaves (Hirano et al., 1995); and for the simulation of the penetration of solid particles into buildings (Chen et al., 1999; Lewis, 1995. For many years, standard dusts have been prepared, with different sizes of particles and different indices of light refraction. These standards have been used for capture effectiveness tests of filtration devices and for tests of optical devices measuring light dispersion on the aerosol particles such as the Arizona Dust, which has been used since the 1940s (SAE, 1943).
One of the first laboratory devices for the testing of dust production from different materials was designed by Andreasen, Hofman-Bang and Rasmusen (Andreasen et al., 1939). Their experiment used a long, thin-walled tube in which they measured the settling time of particles of various materials and deduced their size from Stokes Law. This study also included the first measurements of the fractionation of particles under different conditions, in their case the relative humidity and moisture of the parent material. Their device is considered the precursor of series of modern devices for the production of dust and observation of the free fall of particles of various sizes (Heitbrink et al., 1992; Cheng and Yeh, 1979; Lanning et al., 1995; Sutter et al., 1982). The more recent dust formation devices use the principle of vibration screening (Deichman and Dustshaker, 1944; Sonkin et al., 1946), or produce the dust by means of a scraper breaking the material mounted on a rotating cylinder (Graham et al., 1985; Wright, 1950).
The majority of laboratory methods which deal with the production of dust from a parent material or with resuspension in relation to the atmospheric aerosol (both in the interior and the exterior environment) have one common feature: the physical sampling on the filtration media with a subsequent gravimetric analysis. The references very rarely mention the use of other techniques based on optical sensors (Chen et al., 1999) or TEOM (Tapered-Element Oscillation Microbalance) (Breum et al., 1999; Bussaca et al., 1997). Various technologies used for the suspension of aerosol under laboratory conditions have been summarized in the work of Gill, Zobeck and Stout (Gill et al., 2006).
In this paper I would like to present the results of a complex physical characterization of quartz test aerosol, which was used in the Czech research project SPREAD. The main aim of project SPREAD was to create a useful mathematical model which would simulate the process of the dispersion of aerosol particles after the explosion of a “dirty bomb” in different environments. For these purposes several controlled outdoor explosions of quartz test powder were performed. The incurred dust cloud mass concentration was monitored by six laser nephelometers (DustTracks – 8520, TSI) and a series of passive dosimeters placed downwind on the path of the dust cloud. The obtained concentrations were compared with the dispersion model. The results of the project are presented in the work of Skřehot (Skřehot et al., 2008). To obtain a rough idea about the quartz test powder size distribution and dominant particle diameter I performed several pneumatic suspensions of the powder in the chamber and in-situ monitored the suspended particles with an APS (Aerodynamic Particulate Sizer) analyzer. The aerosol number and mass size distribution statistic are presented in this paper. The median particle diameters were used later in the dispersion model of project SPREAD.
2. Experiment
A resuspension chamber linked to an APS of the Institute for Environmental Studies, Charles University was used for the complex characterization of the physical properties of quartz test particles (mass density 2.4 g·cm3) (see figure 1). The total volume (V) of the chamber was 0.437 m3, the inner surface (S) was 0.35 m2 and the ratio S/V was 8.375. The working section of the chamber was 1.205 m long with a cross section of 0,33 m2. Two asynchronous ventilators were positioned in the center of the chamber walls, opposite each other. Their maximum regulated power was 15 W and they were mounted onto rotating heads, allowing the air flow to be directed (up to 5 m·s-1). The ventilator setting in our study generated a spiral air flow at the sides of the wall from the middle part of the chamber to the top. Individual samples of quartz powder were weighed and placed into a glass tube with four jet openings at the bottom (see figure 2). The tube was inserted into a bushing in the center of the upper base of the chamber. The quartz sample was then pneumatically dispersed without pre-sieving by 0.8 L of dried and clean compressed air from a steel bottle of compressed air (pressure after the first stage 9-10 atm). The velocity of the flow through the jets reached 6 m·s-1. The process of suspension was monitored by a small camera focused on the jets of the suspension tube. Dispersions of the quartz dust were performed at a temperature of 20 °C and RH (relative humidity) 50 %. Figure 2. shows the resuspension of the quartz test powder in the chamber.

Figure 1: Resuspension chamber
The dispersed aerosol was then evaluated by an APS, which was connected to the bottom of the chamber. The aerosol was diluted by clean air, and properties such as number, mass and surface distributions were viewed on-line and recorded as 5 s integrates. Figure 2 shows the suspension of the quartz aerosol.
a
b
Figure 2: Suspension of experimental quartz powder: a) before suspension, b) dust plume during suspension
3. Results and discussion
A total number of 25 dispersions were performed to investigate the proper mass load for dispersion in order to obtain maximum aerosol mass concentration - 5 dispersions for each mass load (10, 25, 50, 75 and 100 mg) under the conditions of 20 ^(o)C and RH (Relative Humidity) 50 %. The density of the quartz test powder was 2.4 g·cm-3. The number concentration of dispersed particulates was high - up to 107 (#·cm3) - therefore the analyzed air was diluted with clean dry air (coefficient of dilution 6.7). The level of resuspension of individual samples of different masses is expressed as a percentage of the measured mass concentration in relation to the maximum possible mass concentration calculated for the individual loads. Table 1 shows the maximum mass concentrations (mg·m-3) for the suspension of different mass samples within the volume of the resuspension chamber.
| Suspended sample mass [mg] | Mass concentration at 100 % suspension [mg·m-3] |
| 10 | 22.88 |
| 25 | 57.25 |
| 50 | 114.41 |
| 75 | 171.62 |
| 100 | 228.83 |
Table 1: Maximum mass concentration of the suspension of 10, 25, 50, 75 and 100 mg symplex; Suspended sample mass [mg]Mass concentration at 100 % suspension [mg·m-3]1022.882557.2550114.4175171.62100228.83
The optimum mass load to obtain maximum mass concentration was 10 mg. On average, maximum mass concentration reached 10 % of its maximum possible load (see figure 3). Figure 3 shows the scatter plot of time-resolved mass concentrations after dispersing 10 mg of quartz powder.
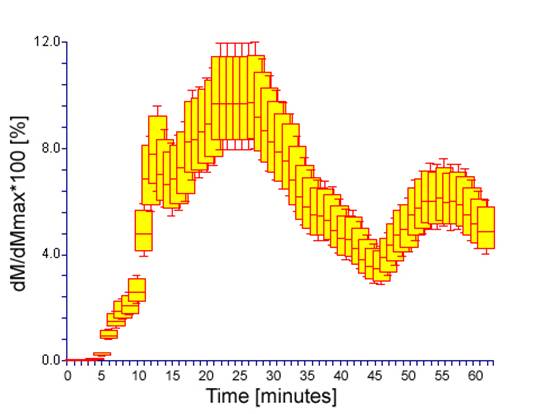
Figure 3: Scatter plot of time-resolved mass concentration after dispersing 10 mg of quartz powder showing maximum, 75th percentile, median, 25th percentile and minimum value for each time period
After the optimal mass load determination, 5 dispersions were performed and recorded in 5 s intervals. About 720 size distributions were gathered, 300 with the highest mass concentration were selected for determination of average number and mass size distribution, which characterizes the state when the maximum number of particulates is dispersed in the chamber (See figure 4).

Figure 4: a) Average number size distribution of aerosol particles, b) Average mass size distribution of aerosol particles
In figure 4a it is seen that the peak with the maximum number of particulates reaches almost 2·104 particulates per cm3 with the diameter 0.7 ?m. The average particulate size in the number-size spectrum is 1.07 μm. Figure 4b shows the mass size distribution and is characterized by several peaks: 1.29 μm (12.3 mg·m-3), 4.7 μm (3.16 mg·m3), 6.7 μm (2.5 mg·m-3) and 11 μm (4.7 mg·m-3). The average particle size in the mass concentration-size spectrum is 2.42 μm. Additional statistical data is listed in table 2.
|
|
Number concentration | Surface area concentration | Mass concentration |
| Median (μm) | 0.976 | 1.34 | 1.65 |
| Average (μm) | 1.07 | 1.60 | 2.42 |
| Geometric average (μm) | 0.994 | 1.39 | 1.90 |
| Modus (μm) | 1.04 | 1.38 | 1.49 |
| Geometric standard deviation | 1.44 | 1.62 | 1.90 |
| Total concentration | 105 (#·cm-3) | 15·103 (μm2·cm-3) | 6.00 (mg·m-3) |
Table 2: Statistical data for the dispersed quartz powder measured by APS
One of the important characteristics of dispersed quartz powder is the deposition velocity in the volume of the chamber, which is essential for the determination of the minimum time used for suspension evaluation. The deposition velocities of different sized particles can be calculated with the basic formula:
N=N0·exp(-?t),
where N is the current number of particles, N0is the initial number of particles, ? is the deposition velocity constant and t is the time. This model can be applied to the data obtained from the APS, while the deposition velocity can be calculated in the following way:
Vd =![]() ,
,
where S and V are geometrical surface and volume of the chamber respectively. Three suspensions of each sample were carried out with the ventilators switched off and on under the conditions of 20 °C and RH of 50 %. The load of the quartz powder mass was 10 mg. Figure 5 shows selected suspensions of the quartz powder with the ventilators switched on and off. During the selected resuspension of the quartz powder with the ventilators switched on, the maximum number concentration was 104 particles per cm3, the aerodynamic particle diameter of dominating particulates was 1.04 μm. The whole measurement took 85 minutes (the first 45 minutes are shown), at the end of which the aerodynamic particle diameter of most dominant particle was only 0.8 μm. During the resuspension of the quartz powder with the ventilators switched off, the maximum number concentration was 104 particles per cm3, and the aerodynamic particle diameter was again dominated by the particle with a diameter of 1.04 μm. This whole measurement took 223 minutes (only the first 45 minutes are shown), at the end of which the aerodynamic particle diameter of the most dominating particle was 0.8 μm, the same as in the previous case.
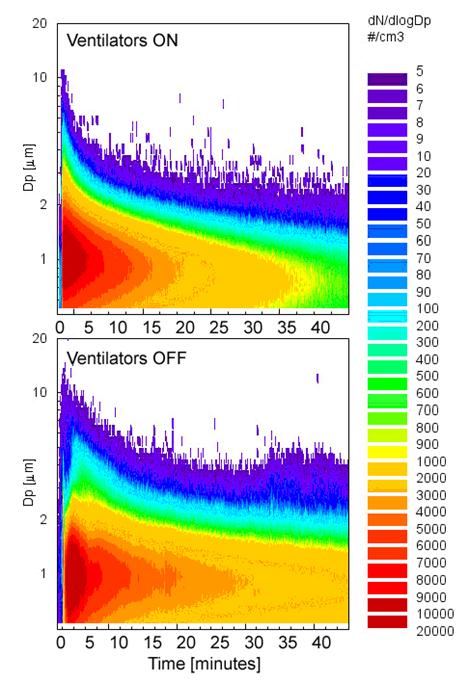
Figure 5: Temporal variation of number size distributions of dispersed quartz powder measured by APS with ventilators switched on and off
After performing all dispersions under defined ventilator conditions, the average deposition velocity was estimated for the particulates which dominate the quartz powder (0.6 – 1.8 μm). Figure 6 shows the calculated deposition velocity for both ventilator conditions.
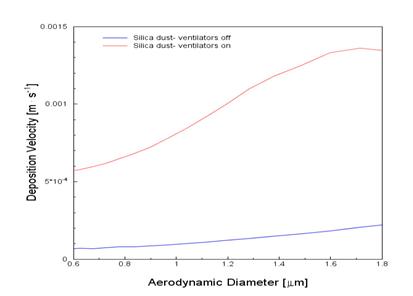
Figure 6: Average deposition velocity of quartz powder measured under conditions of ventilators on and off
It can be seen that air flow (5 m·s-1) increases the deposition of the particles by about 14 times for the particles of size 1.7 μm, while for the particles around size 0.6 μm it is only 6 times. Particles are deposited to the inner surface of the chamber.
The obtained values of the deposition velocity of the quartz powder were compared with the model of sedimentation. The results were computed for mass median particle diameters of the powder sample – 1.07 under the conditions of switched off ventilators. With the previous mathematical assumption, the deposition velocity in still air (ventilators off) for 1.07 μm particle was calculated and resulted in 7.69·10-4 m·s-1. From the model of Terminal settling velocity (Hinds, 1999), where:
VTS=![]() ,
,
for particles of aerodynamic diameter Dp > 1 μm and Re (Reynolds number) < 1.0, where ?p is the particle density, d- particle diameter, g- gravity acceleration and ? viscosity, the sedimentation velocity was determined to be 8.3·10-4 m·s-1. Experimentally obtained deposition velocity differs from the terminal settling velocity model by only 0.61·10-4 m·s-1 and therefore dispersion results correspond very well with the model of sedimentation.
In real atmosphere the deposition of particles is rather more complicated, due to the large number of factors which are not all present in the laboratory environment. Using the Raupach model (Raupach et al., 2001), where:
 ,
,
Vd is the dry deposition velocity, VTS is the terminal settling velocity (the particle has a larger diameter than 1 μm so the Cunningham slip correction factor can be neglected), u*is the friction velocity derived for a surface with grass up to 10 cm in height (0.36 m·s-1) (Lees et al., 1996), ur is the wind speed, af is the empirical parameter (2), St is the Stokes number, ? is the coefficient of the surface type derived for grasslands (1.2) (Zhang et al., 2001), av is the empirical parameter (8) and Sc is the Schmidt number. The dry deposition velocity of particles with diameter 1.07 μm was calculated for velocities of wind from 1-10 m·s-1 (See figure 7). The parameters that were chosen in the model represent the surface field characteristics of the grass field tests performed during project SPREAD.
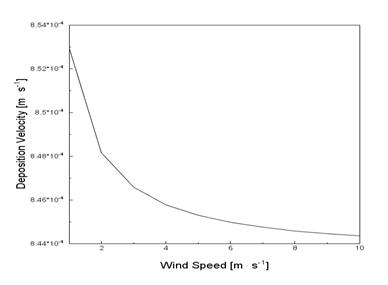
Figure 6: Modeled dry deposition velocity of quartz powder measured in the air above a grass surface calculated for wind speed from 1-10 m·s-1
From figure 6 it is apparent that the deposition velocity decreases with increasing wind speed above the grass surface, therefore in the real atmosphere the deposition velocity is decreased by increasing wind velocity and for a particle with size around 1 μm the deposition velocity is low, so the wind flow and obstacles play the major role in deposition.
4. Conclusion
A resuspension chamber was used to disperse and characterize the quartz powder using the APS in terms of optimal load for dispersion, average size and mass size distribution. Firstly, the optimal sample mass was investigated to obtain the maximum mass concentration after dispersion. With the determined optimal mass sample, the average number size and mass size distributions were obtained together with basic aerosol statistics.
In further dispersion the quartz powder was investigated for the plate-out rate under different conditions - with ventilators switched on and off. The plate-out rate was calculated from the particle decay in time. The plate-out rate of the most common particle, obtained under the condition of switched off ventilators, was compared with the model of terminal settling velocity. The results of the model and measurement correspond with each other.
The Raupach model was used to investigate the deposition velocity under outdoor atmospheric conditions. It was found that for the most common quartz test powder particle size, the deposition velocity decreases with the increasing wind. Particles around this size are easily carried by the wind, and therefore a major role for the deposition of these particles is played by wind flow, turbulence and obstacles.
When performing the dispersions of quartz test powder or any other aerosol in the real atmosphere or working environment using a controlled explosion or during an accident, the deposition velocities of particles around 1 μm are so slow that sedimentation of these particles during short time intervals (a few minutes) can be neglected and only the parameters of the air flow and turbulence need be taken into consideration, because these have the highest influence on the particle transportation and occasional deposition.
Literature
American Society for Testing and Materials. 1984. Effectiveness of Dedusting Agents for Powdered Chemicals. ASTM Designation D-D4331-84. West Conshohochken, PA : ASTM Committee D22.04 on Workplace Atmospheres, 1984. Pp. 448-452.
ANDREASEN, A.H.M.; HOFMAN-BANG, H.; RASMUSSEN, N.H. 1939. On the ability to be dusty of materials. Kolloid-Zeitschrift, 1939, no. 86, 70–77.
BREUM, N.O. 1999. The rotating drum dustiness tester : variability in dustiness in relation to sample mass, testing time, and surface adhesion. Annual Occupational Hygiene, 1999, no. 43, 557–566.
BUSACCA, A.; STETLER, L.; HORNING, L.; BARRY, R.; WAGONER, L.; SAXTON, K.; ASHBAUGH, L.L. 1997. Development of a PM10 ‘dustiness index’ to assess wind erodibility of soils of the Columbia Plateau, Pacific Northwest. In Wind Erosion International Symposium-Workshop, Manhattan, KS, 3–5 June 1997.
CHEN, Y. C.; BARBER, E. M.; ZHANG, Y.; BESANT, R. W.; SOKHANSANJ, S. 1999. Methods to measure dust production and deposition rates in buildings. Journal of Agriculture engineering Research, 1999, no. 72, 329-340.
CHENG, Y.S.; YEH, H.C. 1979. Particle Bounce in Cascade Impactors. Environmental Science Technology, 1979, no. 13, 1392-1396.
CONCESSIO, N. M.; JÄGER-WALDAU, R; HICKEY, A.J. 1997. Aerosol delivery from an active emission multi-single dose dry powder inhaler. Particulate Science Technology, 1979, no. 15, 51-63.
DAHMANN, D.; HARTFIEL, K.; MOCKLINGHOFF, K. 1997. A procedure for the realistic determination of the dust-making inclination of waste. Gefahr. Reinhalt. der Luft, 1997, no. 57, 503-507.
DEICHMAN, W.B.; DUSTSHAKER, A. 1944. Journal of Industrial Toxicology, 1944, no. 26, 334–335.
GILL, E.T.; ZOBECK, T.M.; STOUT, J.E. 2006. Technologies for laboratory generation of dust from geological materials. Journal of Hazardous Materials, 2006, no. 132, 1-13.
GRAHAM, J.A.; MILLER, F.J.; DAVIES, D.W.; HITESHEW, M.E.; WALSH, L.C. 1985. Inhalation studies of Mt. St. Helens volcanic ash in animals I : introduction and exposure system. Environmental Research, 1985, 37, 61–71.
HEITBRINK, W.A.; BARON, P.A.; WILLEKE, K. 1992. An investigation of dust generation by free falling powders. American Industrial Hygiene Association Journal, 1992, no. 53, 617–624.
HINDLE, M.; BYRON, P.R. 1995. Size distribution control of raw materials for dry powder inhalers using the aerosizer with the aero-disperser. Pharmaceutical Technology, 1995, no. 19 (6), 64-78.
HINDS, C.W. 1999. Aerosol Technology, properties, behavior, and measurement of airborne particles. Second edition. New York : John Wiley & sons, 1999.
HIRANO, T.; KIYOTA, M.; AIGA, I. 1995. Physical effects of dust on leaf physiology of cucumber and kidney bean plants. Environmental Pollution, 1995, no. 89, 255-261.
LANNING, J.S.; BOUNDY, M.G.; LEITH, D. 1995. Validating a model for the prediction of dust generation. Particulate Science Technology, 1995, no. 13, 105–116.
LEES, F. 1996. Loss Prevention in the Process Industrie : volume 1. Second edition. Oxford : Butterworth-Heinemann, 1996.
LEWIS, S. 1995. Solid particle penetration into enclosures. Journal of Hazardous Materials, 1995, no. 43, 195-216.
MORALES, J. R.; DINATOR, M. I.; LLONA, F.; SAAVEDRA, J.; FALABELLA, F. 1994. Sample preparation for archeological materials for PIXE analysis. Journal of Radioanalytical Nuclear Chemistry Letters, 1994, no. 187, 79-89.
MUHLE, H.; BELLMANN, B.; CREUTZENBERG, O.; HEINRICH, U.; KETKAR, M.; MERMELSTEIN, R. 1990. Dust overloading of lungs after exposure of rats to particles of low solubility : comparative studies. Journal Aerosol Science, 1990, no. 21, 374-377.
NEWMAN, S. P. 2004. Dry powder inhalers for optimal drug delivery. Expert Opinion on Biological Therapy, 2004, no. 4, 23-34.
NEWMAN, S.P.; BUSSE, W.W. 2002. Evolution of dry powder inhaler design, formulation and performance. Respiration Medicine, 2002, no. 96, 293-304.
RAUPACH, M.R.; BRIGGS, P.R.; AHMAN, N.; EDGE, V.E. 2001. Endosulfan Transport : II. Modeling airborne Dispersal and Deposition by Spray and Vapor. Journal of Environmental Duality, 2001, no. 30, 729-740.
SAE Handbook. 1943. 1943 Edition, Page 716.
SKŘEHOT, P. 2008. Verification of SPREAD model of life : endangering events effects and impacts – SPREAD project. Journal of Safety Research and Application, 2008, vol. 1, no. 3. Available online: <http://www.bozpinfo.cz/josra/josra-03-2008/skrehot_havlova_spread_2.html>.
SONKIN, L.S.; LIPTON, M.A.; HOESON, D. van. 1946. An apparatus for dispersing finely divided dusts. Journal of Industrial Hygiene and Toxicology, 1946, no. 28, 273–275.
SUTTER, S.L.; JOHNSON, J.W.; MISHIMA, J. 1982. Investigation of accident-generated aerosols : releases from free-fall spills. American Industrial Hygiene Association Journal, 1982,no. 43, 540–543.
WRIGHT, B.M. 1950. A new dust-feed mechanism. Journal of Scientific Instruments, 1950, no. 27, 12–15.
ZHANG, L.; DAO, S.; PADRO, J.; BARRIE, L. 2001. A Size–Segregated Dry deposition Schneme for an Atmospheric Aerosol Module. Atmospheric Environment, 2001, no. 35, 549-560.
Vzorová citace:
CIVIŠ, Martin. The resuspension chamber as a tool for complex characterization of the quartz test aerosol. Časopis výzkumu a aplikací v profesionální bezpečnosti [online], 2010, roč. 3, č. 2. Dostupný z WWW: <http://www.bozpinfo.cz/josra/josra-02-2010/resuspension-chamber_civis.html>. ISSN 1803-3687.
Užitečné odkazy
Provozovatel portálu
Jeruzalémská 1283/9
110 00 Praha 1


