Validation possibilities of the BLEVE termal effects
Možnosti validace matematického modelu tepelných účinků jevu BLEVE
Jan Skřínskýa, Guillaume Tetub, Maria Skřínskác, Jan Marekd, Vilém Slukae, Martina Pražákováf, Stanislav Malýg
a Vysoká škola báňská - Technická univerzita Ostrava, jan.skrinsky@vsb.cz
b Ecole des Mines de Douai, guillaume.tetu@minesdedouai.fr
c Vysoká škola báňská - Technická univerzita Ostrava, maria.skrinska@vsb.cz
d Vysoká škola báňská - Technická univerzita Ostrava, jan.marek@vsb.cz
e Výzkumný ústav bezpečnosti práce, sluka@vubp-praha.cz
f Výzkumný ústav bezpečnosti práce, prazakova@vubp-praha.cz
g Výzkumný ústav bezpečnosti práce, maly@vubp-praha.cz ,
Abstract
To understand the accident and at the same time to create a proper emergency scenarios, it is necessary to know the physical nature of emergency events. The aim of this contribution is to describe the possibility of verifying the characteristics of the phenomenon of Fire Ball, as accidental phenomenon, which is often present in major accidents in the industry. At the beginning of the contribution are described the conditions that are necessary or sufficient for its creation. There is also described a simple model for calculating the basic parameters related to this phenomenon - size, diameter, duration, effects distance, etc. In the second part of the contribution three major fire ball accidents using the ARIA and e-MARS databases are described. In the third part of the article description is made of the currently used mathematical models of the phenomenon and a comparison is made of the mathematical model developed and used for this work with the results of experimental simulations, theoretical models and the data from the accident with the occurrence of this phenomenon.
Keywords: BLEVE; Fire Ball; major accident; T.N.O. model; C.C.P.S. model; T.R.C. model
Abstrakt
Ke správnému vytvoření havarijních scénářů a zároveň k pochopení havárií je nutné znát fyzikální podstatu havarijních jevů. První část tohoto příspěvku je zaměřena na popis fyzikálně - chemických charakteristik jevu Fire Ball. Uvedený havarijní jev, je často přítomen při závažných haváriích v průmyslu. Je popsán způsob jeho vzniku, jsou diskutovány podmínky, které jsou nutné nebo postačující k jeho vzniku. Jsou diskutovány základní fyzikálně chemické parametry, vztahující se k tomuto jevu - velikost, průměr, doba trvání apod. Dále je popsán způsob, jakým se může prostředím šířit nebezpečí, které ohňová koule představuje. V druhé části příspěvku je uveden souhrn tří závažných havárií s výskytem tohoto jevu z databází ARIA a e-MARS. Je proveden výčet a množství látek, které tento jev způsobily. Jsou uvedena množství, ve kterých se látka při vzniku ohňové koule vyskytovala a popsán dosah nebezpečí ve formě množství – tepelný tok – vzdálenost. Ve třetí části příspěvku je proveden popis matematicko- fyzikálních parametrů modelů tohoto jevu. Ve čtvrté části je popsáno porovnání modelu s výsledky experimentálních studií.
Klíčová slova: BLEVE; Fire Ball; závažná havárie; T.N.O. model; C.C.P.S. model; T.R.C. model
Introduction
Hydrocarbon fuels are being stored under high pressure on an increasing scale worldwide. Accidental loss of containment causes rapid mixing of fuel with the air and formation of a flammable cloud capable of exploding or burning as a Fire Ball. The event starts with a major failure of the container. Because the pressure in the container is greater than atmospheric pressure, much of the liquid is quickly expelled into the atmosphere. In response to this rapid drop in pressure, a portion of the liquid flashes to vapor nearly instantaneously. This vapor expands rapidly, shattering some of the remaining liquid into small drops, thereby creating a turbulent aerosol cloud consisting of vapor, liquid drops, and air. The aerosol cloud quickly increases in size, entraining more air as it grows. Ignition of aerosol cloud results in a Fire Ball that exists until the vapor and liquid fuel within the cloud are consumed. The Fire Ball can emit a large amount of radiant energy during its brief life, and is capable of causing injuries and damage over an area several times greater than the size of the Fire Ball. Therefore, when conducting a hazards or risk analysis of process vessels or storage tanks that contain superheated flammable liquids, it is important to be able to accurately model the radiant heat effects of Fire Balls [1].
Previous experimental research
Small scale experiments
The first experimental study published in literature has been made by [2] in the late 80s. She used 1 liter commercial reservoir filled either with propane (C3H8) or with R12 (CCl2F2). The reservoirs were heated from below by a propane torch, the rupture was initiated by the impact of a 0.22 inch bullet. In [3] were performed a large series of BLEVE experiments using the same type of 1 liter commercial reservoir as McDevitt, but heated by a pool fire, until rupture. He used 10 different liquids and the rupture conditions were changed by drilling a weakness on the reservoir. In 2003, [4] performed BLEVE with 5 and 11kg propane reservoirs heated from below by gas burners until rupture. He also measured the internal pressure of the reservoir that was supercritical before rupture, i.e. above the critical point of the fuel.
Middle scale experiments
In 2007, Birk published a series of experiments that were performed between 2001 and 2004 with 2000 l ASME code propane tanks [5]. Internal pressure, temperatures at different positions inside the reservoir and overpressures at 10 m to 40 m both at side and end directions from the reservoir have been measured. During heating of the reservoir, the pressure relief valve connected to the reservoir opened before the vessel rupture, once the internal pressure has exceeded the valve design pressure, set to 1.72 MPa. Therefore, a certain quantity of propane was ejected prior rupture, decreasing the percentage of the fluid remaining inside the reservoir to 15-60%, depending on the test. In the article [5], the author gives the conditions at rupture and the corresponding overpressures at different distances and directions.
Large scale experiments
In 1991, 7 large scale experiments were performed by British gas in the frame of a European commission research project and published by [6]. The reference case was a 5 and 6 m3 reservoir, containing 2 tons of butane that was heated until a pressure of 15 bars, and then ruptured by detonation of a linear shape explosive. The overpressure was measured at 25, 50, 75, 100 and 150 m from the source, in different directions. A few years later, the Federal institute of material research and testing (BAM) in Germany performed a test with a 45 m3 reservoir, filled at 22% (5 tons) with propane [8]. It ruptured at 25 bar after being immersed in a hydrocarbon pool fire. The blast wave was recorded at 100, 150 and 200 m from the source.
Previous studies on accidents
For the present investigation more than 70 references could be find in the database ARIA (Analyse, Recherche et Information sur les Accidents) provided through the BARPI (Bureau d’Analyse des Risques et Pollutions Industrielles) and e-Mars (Major Accident Reporting System later renamed to e-MARS) concerning the BLEVE Fire Ball. The most cited accidents are Feyzin, France, 1966 and Texas city, USA, 1978. For the experimental simulation and theoretical models validation the (1) Los Alfaques, Spain, 1978, (2) San Juan Ixhuatepec, Mexico, 1984 and (3) Kamena Vourla, Greece, 1999 accidents data were chosen because of the relevant data for the semi-empirical model presented.
Los Alfaques, Spain, 11/07/1978
A truck carrying 23.5 tons of propylene hit the wall of a camping spot 700 to 800 vacationers. The tank was cracked and inflammation of rejection gas which was formed causes an increase in the internal pressure and deterioration of the tank walls. Following an initial explosion, BLEVE occurs including generating a Fire Ball. This accident was the cause of 216 deaths and more than 200 injured in a radius of 125 m. It should be noted that the truck was filled with a quantity of propylene over capacity allowed (23.5 tons against 19.1 tons), and was not provided with a valve [10].
San Juan Ixhuatepec, Mexico, 19/11/1984
The storage consisted of four spheres of LPG (80% butane mixture, 20% propane) with a unit volume of 1600 m3, two spheres of 2400 m3 volume and 48 horizontal cylindrical tanks of various capacities. At the time of the accident, approximately 11000-12000 m3 LPG were stored on the site. During a phase of filling a reservoir, a pipe of 200 mm diameter fewer than 24 bar breaks. When the height of the cloud reached a height visible about two meters, it ignites, 5 to 10 minutes after the beginning of the leak, a flare located some 120 to 150 meters from the location of the release. The flammable cloud with probably entered the houses, the inflammation leads to destruction. A few minutes after ignition of the cloud, two smaller spheres give BLEVE material, causing the formation of a Fire Ball (diameter measured without certainty, 350 or 400 meters) and the ejection of one or two cylindrical tanks. Ultimately, the four small spheres were destroyed. Larger spheres remained intact, although their Bracketing was broken. Only 4 of the 48 cylinders remained in their initial position. Within a radius of 300 meters, all the people were killed or injured. The accident caused the death of a total of more than 500 people. There were about 7000 injured and 39,000 people evacuated. Relief mobilized around 4,000 people. Fragments were found in areas more than 600 meters and 12 parts of tanks horizontal cylindrical were projected by "rocket effect" at distances up to 1,200 meters [10].
Kamena Vourla, Greece, 30/04/1999
On the eve of public holidays, it is customary that the Greek police ban traffic trucks on the entire road network. On the eve of May 1, the police arrested a truck tank containing 18 tons of LPG near the town of Kamena Vourla. Shortly after, a van comes hit the truck to the rear, causing a leak of LPG which immediately ignites. Thirty minutes later, a vehicle fire just take position 5 m from the tank, a BLEVE occurs. Witnesses reported the formation of a Fire Ball about 100 m radius and 150 m high. Large drops of liquid LPG fire showered over distances of 300 to 400 m. The tanker truck and firefighters completely disintegrated. Large fragments are found at distances of 200 to 300 m (driving the fire truck was found at 250 m). The LPG tank is projected into a one piece in a remote building of approximately 500 m, demolished the roof and landed 300 m away, or at a distance of 700 to 800 m from the explosion. The accident is four people, including a person beheaded by a fragment at 400 m from the explosion. People located 300 m from the accident injured by burns [10].
Mathematical models
C.C.P.S. (Centre for Chemical Process Safety) model [7], (2) solid flame T.N.O. (The Netherlands Organization of applied Scientific Research) model [8] and T.R.C. (Thornton Research Center, Shell) model sometimes called the model of Shield [11-12] and we adopted both C.C.P.S. and T.N.O. models for calculation of the effect distances directly from the mass of flammable liquid in Fire Ball. T.R.C. is well described in literature [11-12].
C.C.P.S. (Centre for Chemical Process Safety) Model
Radiation per unit area received by the receptor:
![]() (1)
(1)
where q = radiation per unit area received by the receptor [W/m2]; ?a = atmospheric transmissivity [-]; R = radiative fraction of heat of combustion [-]; Hc = heat of combustion [J/kg]; mf = mass of fuel in the Fire Ball [kg]; and L = distance from Fire Ball center to the receptor [m].
Distance from Fire Ball center to the receptor:
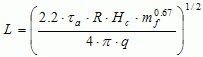 (2)
(2)
where L = distance from Fire Ball center to the receptor [m]; q = radiation per unit area received by the receptor [W/m2]; ?a = atmospheric transmissivity [-]; R = radiative fraction of heat of combustion [-]; Hc = heat of combustion [J/kg]; and mf = mass of fuel in the Fire Ball [kg].
Height of the Fire Ball center from the ground:
![]() (3)
(3)
where H = height of the Fire Ball center from the ground [m]; D = Fire Ball diameter [m]; and mf = mass of fuel in the Fire Ball [kg].
Distance from the Fire Ball center projection to the ground to the receptor:
![]() (4)
(4)
where X = distance from the Fire Ball center projection to the ground to the receptor [m]; L = distance from Fire Ball center to the receptor [m]; and H = height of the Fire Ball center from the ground [m].
For the evaluation of the exposure duration for Fire Ball model we used relationships, which are given in [8]. The equation for Fire Ball duration normally has the following form, which relates the duration or lifetime of the Fire Ball to the mass of fuel involved in the Fire Ball:
![]() (5)
(5)
where t = Fire Ball duration [s]; k, n = constants; and mf = mass of the flammable material in the Fire Ball [kg].
In published models, values of the constants k and n range from 0.23 to 2.61, and from 0.0966 to 0.333, respectively. The [7] version of this equation used in this article is as follows:
![]() < 37000 kg (6)
< 37000 kg (6)
![]() > 37000 kg (7)
> 37000 kg (7)
where t = Fire Ball duration [s]; and mf = mass of fuel in the Fire Ball [kg].
The damage caused by the thermal radiation is proportional to radiation intensity to the four-thirds power times time of exposure [9]:
![]() (8)
(8)
where D = thermal radiation dose [(W/m2)4/3.s]; t = duration of exposure [s]; and q = radiation per unit area received by the receptor [W/m2].
The probit functions for the thermal “dose” that could cause the first-degree burns:
![]() (9)
(9)
where P = probit function [-]; t = duration of exposure [s]; and q = radiation per unit area received by the receptor [W/m2].
T.N.O. (The Netherlands Organization of applied Scientific Research) Model
The amount of liquefied gas released in case of complete failure of the tank:
![]() (10)
(10)
where m = mass of the flammable material [kg]; f = fraction of the volume of the pressure tank, filled with the flammable liquefied pressurized gas [-]; V = volume of the tank [m3]; Vrel = amount of dangerous substance which will be released in case of a complete tank failure [m3]; ? = density of the flammable material in the pressure tank [kg/m3].
The radius of the fireball amount of liquefied gas released:
![]() (11)
(11)
where r = radius of the Fire Ball [m]; m = mass of the flammable material [kg].
The duration of the fireball:
![]() (12)
(12)
where t = duration of the Fire Ball [s]; m = mass of the flammable material [kg].
The lift-off height of the Fire Ball:
![]() (13)
(13)
where H = height from the center of the Fire Ball to the center of the ground under the Fire Ball [m]; r = radius of the Fire Ball [m]; m = mass of the flammable material [kg].
Calculation of the distance X from the center of the Fire Ball to the object:
![]() (14)
(14)
where X = the distance measured over the ground from the projected center of the Fire Ball on the ground under the Fire Ball [m]; H = height from the center of the Fire Ball to the center of the ground under the Fire Ball [m]; x = distance from the center of the Fire Ball to the radiated object [m].
Calculation of the maximum value of the view factor at a distance X:
![]() (15)
(15)
where F = geometric view factor [-]; r = radius of the Fire Ball [m]; X = distance from the center of the Fire Ball to the radiated object [m].
Calculation of the fraction of the generated heat radiated by a Fire Ball:
![]() (16)
(16)
where f = fraction of the generated heat radiated by a Fire Ball [-]; P = vapor pressure of flammable material inside the vessel [Pa].
The net available heat for radiation:
![]() (17)
(17)
where ?H = net available heat [J/kg]; ?HC = combustion heat of the flammable material at its boiling point [J/kg]; ?Hv = vaporisation heat of the flammable material at its boiling point [J/kg]; Cp = specific heat capacity at constant pressure [J/kg.K]; ?T = temperature difference between flame and ambient temperature [K].
The surface emissive power:
![]() (18)
(18)
where E = surface emissive power which is the average radiation emittance of the flame surface [W/m2]; ?H = net available heat [J/kg]; m = mass of the flammable material [kg]; f = fraction of the generated heat radiated by a Fire Ball [-]; r = radius of the Fire Ball [m]; t = duration of exposure [s].
Actual path length between the surface area of the Fire Ball and the object:
![]() (19)
(19)
where x = distance from the center of the Fire Ball to the radiated object [m]; X = the distance measured over the ground from the projected center of the Fire Ball on the ground under the Fire Ball [m]; r = radius of the Fire Ball [m].
Partial vapor pressure of water in air at a relative humidity:
![]() (20)
(20)
where Pw = partial vapor pressure of water in air at a relative humidity RH [Pa; N/m2]; RH = relative humidity of air [%rel/100]; Ta = absolute temperature of ambient air at standard conditions [K].
Calculation of the atmospheric transmissivity (valid for 104 < Pw · x < 105) if absorption coefficient of water vapor and absorption coefficient of carbon dioxide is not known:
![]() (21)
(21)
where ? = atmospheric transmissivity [-]; Pw = partial vapor pressure of water in air at a relative humidity RH [Pa; N/m2]; x = distance from the center of the Fire Ball to the radiated object [m].
The heat flux at a certain distance from the center of the Fire Ball:
![]() (22)
(22)
where q = heat flux at certain distance [W/m2]; E = surface emissive power which is the average radiation emittance of the flame surface [W/m2]; ? = atmospheric transmissivity [-].
Results of calculations
Comparison of calculations with experimental simulations
| Parameter | Unit | Experimental | Theoretical | ||
|
British Gas simulation |
C.C.P.S. model |
T.N.O. Model |
T.R.C. model |
||
| FB maximal diameter | m | 74 | 79 | 82 | 83 |
| FB time of life | s | 6.1 | 6.1 | 6.5 | 5.9 |
| average heat flux | m | 356 | 350 | 256 | 440 |
| high of FB centre | kW/m2 | 85 | 39 | 82 | 77 |
| distance to 1000 (kW/m2)4/3.s | m | - | 98 | 24 | 60 |
Table 1. Comparison of Fire Ball experimental simulation by British Gas with different model.
1 BG = British Gas; chemical name = butane; V = 10796 m3; mf = 2 t; filling degree = 40%; time to ignition = 0.4 s; time to development of maximal diameter = 1.5 s; time to ascension = 3.6 s; time to extinction = 6.5 s
| Parameter | Unit | Experimental | Theoretical | ||
|
B.A.M. simulation |
C.C.P.S. model |
T.N.O. model |
T.R.C. model |
||
| FB maximal diameter | m | 100 | 100 | 104 | 94 |
| FB time of life | s | 7.2 | 7.8 | 7.9 | 7.4 |
| high of FB center | m | 100 | 50 | 104 | 98 |
| average heat flux | kW/m2 | - | 350 | 325 | 332 |
| distance to 1000 (kW/m2)4/3.s | m | - | 136 | 75 | 60 |
Table 2. Comparison of Fire Ball simulation by B.A.M. with different model
1 B.A.M. = Bundesanstalt für Materialforschung und -prüfung; chemical name = propane; V = 45 m3; mf = 5141 kg; rupture pressure = 25 bar; time to ignition = 0.4 s; time to development of maximal diameter = 3.2 s; time to ascension = 4.0 s; time to extinction = 7.6 s
|
filling degree (%) |
Released mass (kg) |
Life-time (s) |
|||
| Experimental | Theoretical | ||||
|
J.I.V.E. simulation |
C.C.P.S. model |
T.N.O. model |
T.R.C. model |
||
| 20 | 279 | 3 | 2.9 | 3.7 | 3.3 |
| 41 | 710 | 5 | 4 | 4.7 | 4.6 |
| 60 | 1272 | 6.5 | 4.9 | 5.5 | 5.7 |
| 85 | 1708 | 7 | 5.4 | 5.9 | 6 |
Table 3. FB life-time calculated for different models for J.I.V.E. experimental simulation
1 J.I.V.E. = Jet fire Interaction with VEssels containing pressurized liquide; chemical name = propane; V = 4.5 m3; mf = 8000 kg; rupture pressure = 25 bar; time to ignition = 0.4; time to development of maximal diameter = 3.2 s; time to ascension = 4.0 s; time to extinction = 7.6 s
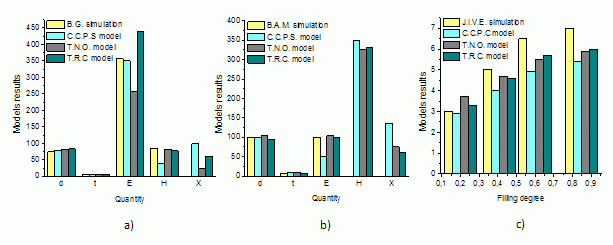
Figure 1. Comparison of calculations with experimental simulations: a) British Gas (B.G.), b) Federal Institute for Materials Research and Testing (B.A.M.), c) Hazard consequences of jet fire interactions with vessels containing pressurized liquids (J.I.V.E.)
Comparison of calculations with accident observations evaluation
| Parameter | Units | Observations | Theoretical | ||
|
C.C.P.S. model |
T.N.O. Model |
T.R.C. model |
|||
| FB maximal diameter | (m) | 300 | 422 | 424 | 406 |
| FB time of life | (s) | 20 | 22 | 24 | 31 |
| average heat flux | (kW/m2) | - | 350 | 392 | 344 |
| high of FB center | (m) | - | 211 | 424 | 411 |
Table 4. Simulation of San Juan Ixhuatepec, Mexico, Mexique, 19/11/1984 accident
| Parameter | Units | Observations | Theoretical | ||
|
C.C.P.S. model |
T.N.O. model |
T.R.C. model |
|||
| FB maximal diameter | (m) | 200 | 152 | 157 | 182 |
| FB time of life | (s) | - | 12 | 11 | 9.6 |
| average heat flux | (kW/m2) | - | 350 | 333 | 563 |
| high of FB center | (m) | 150 | 76 | 157 | 132 |
Table 5. Simulation of Kamena Vourla, Greece, 30/04/1999 accident
| Parameter | Units | Observations | Theoretical | ||
|
C.C.P.S. model |
T.N.O. model |
T.R.C. model |
|||
| FB maximal diameter | (m) | < 200 | 166 | 170 | 167 |
| FB time of life | (s) | - | 13 | 12 | 14 |
| average heat flux | (kW/m2) | - | 83 | 170 | 198 |
| high of FB center | (m) | - | 350 | 302 | 273 |
Table 6. Simulation of Los Alfaques, Spain, 11/07/1978 accident.
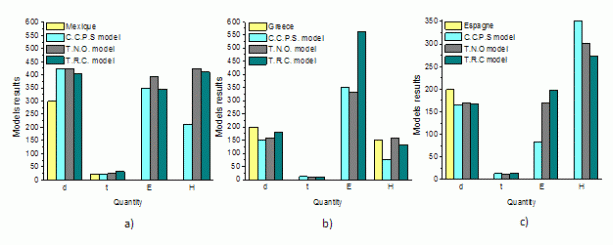
Figure 2. Comparison of calculations with accident observations evaluation: a) Mexico (1984), b) Greece (1999), c) Spain (1978)
Both, in Tables 1-6 and Figures 1-2 are summarized (1) comparison of calculations with experimental simulations and (2) comparison of calculations with accident observations evaluation. All the results are illustrative and should give us the approximate framework of possible solution rather than accurate and precise values. On the other hand, from given illustrative results could be well established the trends based on the comparison of C.C.P.S. simple point source and T.N.O. and T.R.C. solid flame models, trends between the results of the experimental simulations and the trends between the accidents observations that occurs between the presented estimations. At the same time could be deduced the cross over trends between calculations, experimental results and observations evaluation. All the results of the simplified calculation results could be at the same time used as the input data for more rigorous models.
Conclusion
The historical survey performed on the accidents occurred indicates that accidents with Fire Ball from BLEVE are very frequent, have high impact and high consequences. On the other hand, there are only limited numbers of experimental simulations performed with limited kinds of chemical substances. The objective of the contribution was to summarize the understanding, the modeling and the validation of fireball from Fire Ball appearance and consequences. From the information about the experimental data presented we can summarized that there is only a very limited number of studies applicable to the validation of simple mathematical-physical models. This data are highly dependent on the experimental conditions (atmospheric conditions, etc.). However, they can give us at least the frame of information for the purposes of validation in part. Regarding the number of the studies, the most studies have been performed to study the phenomenon Fire Ball was mainly medium- and large-dimensional experiments, fewer studies have been made to study this phenomenon in the small scale. From the point of view of accidents number, a similar trend can be obtained for Fire Ball accidents observation. The largest number of Fire Ball major accidents can be found in ARIA and e-MARS databases, some other accidents descriptions could be found in journal articles. Regarding the difficulty of assessing the use of introduced semi-empirical point source model in terms of its performance on the input and output data could be concluded that it is possible to apply this model for emergency planning. In compare to modified C.C.P.S. model using the modified T.N.O. and T.R.C. model is very limited because of the input data with respect to the geometric factor of the target, the determination of the emission radiation flux from the surface of the flame and the atmospheric transmissivity with average flame temperature. Therefore, as a more suitable possibility is to use a simple point source model, in which all of these problems fall away. By this model we calculate only the value of the heat flux corresponding to the effect and calculate the distance from the fire to the target (recipient). Simply by comparing the modeling results between them can lead to results that differ from 40% to 70% (the values of point source model calculations overestimate the distance measured over the ground from the projected center of the Fire Ball on the ground under the Fire Ball see Table 1-2 and Figure 1 a,b), which is consistent with published results. A similar agreement can also be found by comparing the calculated results with the results of presented experiments and observations in accidents.
Acknowledgement
The contribution was prepared in the frame of following projects:
1. Opportunity for young researchers, reg. no. CZ.1.07/2.3.00/30.0016,supported by Operational Programme Education for Competitiveness and co-financed by the European Social Fund and the state budget of the Czech Republic;
2. Optimization of emergency planning zone and emergency plans creation based on harmful effects of dangerous chemicals released during major accidents with respect to improvement of civil protection reg. no. VG20112013069, supported by Ministry of Interior of the Czech Republic;
3. Innovation for Efficiency and Environment, reg. no. CZ.1.05/2.1.00/01.0036 supported by Operation Programme Research and development for Innovation and financed by the Ministry of Education, Youth and Sports.
Literature
[1] VENART, J.E.S. …[et al.]. An Anatomy of a Boiling Liquid Expanding Vapour Explosion. Process Safety Progress, 1993, Vol. 12, No. 2, 1993, pp 67-71.
[2] McDEVITT, C.A.; STEWARD, F.R.; VENART, J.E.S. Boiling liquid expanding vapour explosion : an update. In 5th Technical Seminar on Chemical Spills, Montreal. Pergamon Press, 1988.
[3] RIRKSOMBOON, T. Investigation of small BLEVE tests. PhD thesis. University of New Brunswick, 1997.
[4] STAWZYK, J. Experimental evaluation of LPG tank explosion hazards. Journal of Hazardous Materials, 2003, Vol. 96, No. 2, pp. 189-200.
[5] BIRCK, A.M.; DAVISON, C.; CUNNINGHAM, M.H. Blast overpressures from medium scale BLEVE tests. Journal of Loss Prevention in the Process Industries, 2007, Vol. 20, No. 3, pp. 194-206.
[6] JOHNSON, D.M.; PRITCHARD, M.J. A large scale experimental study of BLEVEs. British Gas plc, Research and Technology Division, 1991.
[7] US EPA. Risk Management Program Guidance for Offsite Consequence Analysis : Appendix C : Flammable Substance. US EPA, 1999.
[8] TNO Bureau for Industrial Safety, Netherlands Organization for Applied Scientific Research. Methods for the Calculation of the Physical Effects. Hague : Committee for the Prevention of Disasters, 1997.
[9] TNO Bureau for Industrial Safety, Netherlands Organization for Applied Scientific Research. Methods for the Determination of Possible Damage. Hague : Committee for the Prevention of Disasters, 1992.
[10] LEES, F.P. Loss Prevention in the Process Industries. Butterworth Heinemann, 2001.
[11] SHIELD, S.R. A Model to Predict Radiant Heat and Blast Hazards from LPG BLEVES. In AIChE 29th National Heat Transfer Conference, August 1993. Pp. 139-149.
[12] SHIELD, S.R. Consequence Modeling for LPG Distribution in Hong Kong : Research Note TNRN.95.7001. Thornton Research Centre, December 13, 1994.
Vzorová citace
SKŘÍNSKÝ, Jan …[et al.]. Validation possibilities of the BLEVE termal effects. Časopis výzkumu a aplikací v profesionální bezpečnosti [online], 2013, roč. 6, č. 2. Dostupný z WWW: <http://www.bozpinfo.cz/josra/josra-02-2013/bleve.html>. ISSN 1803-3687.
Užitečné odkazy
Provozovatel portálu
Jeruzalémská 1283/9
110 00 Praha 1


