Description of physical-chemical parametres of Pool-fire
Popis fyzikálně-chemických parametrů jevu pool fire
Jan Skřínskýa, Mária Skřínskáb, Jan Marekc, Vilém Slukad, Martina Pražákováe, Stanislav Malýf
aVysoká škola báňská - Technická univerzita Ostrava, jan.skrinsky@vsb.cz
bVysoká škola báňská - Technická univerzita Ostrava, maria.skrinska@vsb.cz
cVysoká škola báňská - Technická univerzita Ostrava, jan.marek@vsb.cz
dVýzkumný ústav bezpečnosti práce, sluka@vubp-praha.cz
eVýzkumný ústav bezpečnosti práce, prazakova@vubp-praha.cz
fVýzkumný ústav bezpečnosti práce, maly@vubp-praha.cz,
Abstract
If containment of a flammable liquid is lost and the consequent vapor-air mixture is ignited, estimation of radiation from thermal radiation generated depends upon number of factors. The point source model for the prediction of thermal radiation from liquid pool fires was adopted for the evaluation of the effect distances of Pool Fire we modified the simple point source model for calculation of the effect distances directly from the mass of flammable liquid in Pool Fire. The point source model considers the heat source (i.e. the flame) as a point that emits in all directions. The original model considers the heat received by the observer as a fraction of the heat of combustion multiplied by the burning rate. This heat decreases with the square of the distance from the source and with the transmissivity of the ambient air. In the presented model we implemented different possibilities of heat fraction calculation and we introduced the flame length in order to calculate the point source-target distance. Finally we do not consider the atmospheric stability as s constant but we introduced simple mathematical correlation and compare both the model with and without this parameter. The modified relationship was compared with experimental results and discussion of results is performed.
Keywords: POOL-FIRE; major accident; C.C.P.S. model; ethanol
Abstrakt
Pokud dojde ke ztrátě obsahu a následné iniciaci směsi páry kapaliny se vzduchem, pak stanovení hustoty tepelného toku z tepelného záření závisí na množství faktorů. Odhad hustoty tepelného toku tepelného záření generovaného vzniklým požárem závisí na mnoha faktorech. Pro vyhodnocení efektu tepelného záření požáru v kruhové jímce byl vybrán a modifikován model bodového zdroje. Tento model je možné upravit do tvaru pro výpočet havarijních vzdáleností přímo z hmotnosti hořlavé kapaliny v havarijní jímce. Model bodového zdroje bere v úvahu fyzikální model zdroje tepla (tj. plamene) jako bodu, který vyzařuje se stejnou intenzitou tepelného záření ve všech směrech. Původní model uvažuje teplo, které absorbuje cíl (člověk) jako zlomek spalného tepla vynásobený rychlostí odhořívání. Hodnota toho tepla se snižuje se čtvercem vzdálenosti od zdroje a s propustností okolní atmosféry. V popisovaném modelu jsme realizovali různé možnosti výpočtu frakce tepelného záření a zavedli jsme parametr délky plamene pro výpočet výšky bodového zdroje. Nakonec jsme místo v původním modelu konstantní hodnoty atmosférické stability zavedli jednoduchý matematický vztah aproximující konstantní hodnotu jednoduchou funkcí. Uvedený modifikovaný vztah jsme porovnali s experimentálně získanými hodnotami a provedli diskuzi výsledků.
Klíčová slova: POOL-FIRE, závažné havárie, C.C.P.S. model, ethanol
Introduction
Safety is one of the most important factors in chemical process plants. All operations and processes must be carried out under safe conditions in order to protect the environment. Among the commonly occurring major accidents in chemical process plant are Pool Fires. Pool Fire occurs when a flammable liquid spills onto the ground and is ignited. Fire in a liquid storage tank is also a form of Pool Fire. A pool fire can be defined as s turbulent diffusion fire burning above a horizontal pool vaporizing flammable material under conditions where the flammable material has zero or very low initial momentum (this definition is used for the purpose of this work). A key feature of these fires is that there is a degree of feedback between the fire and the flammable material. To a greater or lesser extend, there is a heat transfer back from the fire to the pool that influences or even controls the rate of evaporation and hence the fire size and other characteristics. The pool with flammable material is not necessarily static. It may be spreading or contracting. Additional flammable material could be coming from a leak. Depletion of the local flammable material supply can occur via drainage or overflow to other areas – perhaps giving tide to running liquid fires. The fundamental subject of fire research with problems involving hydrocarbon pool fires focuses on thermal radiation from the flame surface. The aim of the presented approach is to provide immediate, simple and practical engineering estimates of the radiation hazard.
Previous studies
Over the last few decades there have been numerous experimental studies conducted to establish thermal radiation models from large pool fires [1-7]. To address the above subject, it is necessary to consider how big and fast the fire is burning as well as the consequent effect of smoke on radiation and wind on the resultant flame shape. Systematically, one may look at the operating fire regime that characterizes the scope within which radiation is seen to dominate in heat transfer. Full-scale experimental investigation of heat transfer to objects in or near pool fires is limited because such experiments are expensive and difficult to instrument due to the harsh environment. Consequently, pool fire dynamics and heat transfer have been studied in small-scale, controlled laboratory settings, where detailed instrumentation yields high quality, quantitative data that is used to gain insight into the fire physics and the heat transfer process. The heat flux transferred from the same to the fuel surface has first been expressed by Hottel [8]. In 1959, the author analyzed the results of a systematic study on pool fires, with the liquid surface at the rim of the container (no lip height) and with pool diameters ranging from 3.7 10-3 m to 22.9 m, performed by Blinov and Khudiakov [9]. From his analysis, Hottel assumed that the total heat flux transferred from the flame (at a temperature TF ) to the fuel surface (at a temperature Tf ) is the sum of three heat transfer mechanisms: conduction through the reservoir walls, convection to the fuel surface and radiation from the flame to the fuel. An extensive summary of research in the area of thermal radiation from large fires is contained in the chapter in the Society of Fire Protection Engineers (SFPE) Handbook entitled, Fire Hazard Calculations for Large Open Hydrocarbon Fires [9]. A summary of various calculation methods is included in the SFPE Engineering Guide entitled, Assessing Flame Radiation to External Targets from Pool Fires, published in June, 1999 [10]. The methodology to be described in the present report is not dramatically different from those in the SFPE Engineering Guide. However, in order to maintain the simplicity of the original HUD methodology, it has been necessary to adopt a slightly different approach that emphasizes global energy conservation as a way of minimizing errors in radiation flux predictions due to uncertainties in the measurements upon which the flux calculations are based.
Mathematical model description
The presented model has been simulated numerically within Java and NetBeans environment to provide both the heat flux and distance dependence.
Radiation per unit area received by the receptor:
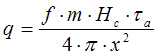 (1)
(1)
where q = radiation per unit area received by the receptor [kW/m2]; f = fraction of heat of combustion radiated [-]; m = rate of combustion [kg/s]; Hc = heat of combustion [J/kg.K]; ?a = atmospheric transmissivity [-]; and x = distance from point source to receptor [-].
The f parameter is difficult to model. Experimental values can be found in literature, but are fuel dependent and a few studies about diesel pool fire are available. According to the C.C.P.S. [1], the fraction of heat of combustion ranges between 0.1 and 0.4. Other authors [2] have also proposed correlations (A-for heptane, crude oil, and kerosene; and B-for diesel, based on curve fitting of experimental data, and depending on the reservoir diameter.
A) ![]() (2)
(2)
where f = fraction of the generated heat radiated by a Pool Fire [-]; and D = circular reservoir Pool Fire diameter [m].
B) 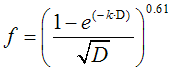 (3)
(3)
where f = fraction of the generated heat radiated by a Pool Fire [-]; and D = circular reservoir Pool Fire diameter [m].
For circular pools the heat source can be considered to be cylindrical. In case of a rectangular or a nearly rectangular pool, for a ratio length/width smaller than 2, an equivalent or effective pool diameter D can be calculated, which is defined with:
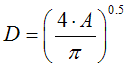 (4)
(4)
where D = circular reservoir Pool Fire diameter [m]; and A = pool area [m2].
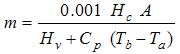 (5)
(5)
where m = rate of combustion [kg/s]; Hc = heat of combustion [J/kg]; A = pool area [m2]; Hv = heat of vaporization [J/kg]; Cp = liquid heat capacity [J/kg];Tb = boiling temperature [K]; and Ta = ambient temperature [K].
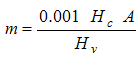 (6)
(6)
where m = rate of combustion [kg/s]; Hc = heat of combustion [J/kg]; A = pool area [m2]; and Hv = heat of vaporization [J/kg].
The empirical Equation 5 is used for estimating the combustion rate of a flammable substance with a boiling point above the ambient temperature, while the Equation 6 is used for the flammable substance with a boiling point below the ambient temperature.
Partial vapor pressure of water in air at a relative humidity:
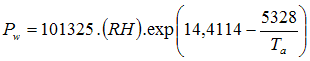 (7)
(7)
where Pw = partial vapor pressure of water in air at a relative humidity RH [Pa; N/m2]; RH = relative humidity of air [%rel/100]; Ta = absolute temperature of ambient air at standard conditions [K].
Calculation of the atmospheric transmissivity (valid for 104 < Pw · x < 105) if absorption coefficient of water vapor and absorption coefficient of carbon dioxide is not known:
![]() (8)
(8)
where ? = atmospheric transmissivity [-]; Pw = partial vapor pressure of water in air at a relative humidity RH [Pa; N/m2]; x = distance from the center of the Fire Ball to the radiated object [m].
Among the correlations that predict the average flame length, most of them show a dependency with the reservoir diameter (D), the burning rate (m):
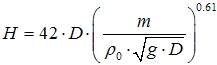 (9)
(9)
where H = mean flame length [m]; D = circular reservoir Pool Fire diameter [m]; m = mass burning rate per unit area [kg.m2/s]; and ρ0 = ambient air density [kg/m3].
Combining Equations 1 and 5, give the following Equation for liquid pools of substances with boiling points above ambient temperature and the value of fraction equal to 0.4 and τ = 1:
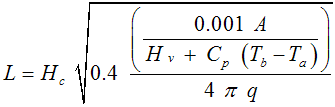 (10)
(10)
where L = distance from Pool Fire center to the receptor [m]; Hc = heat of combustion [J/kg]; A = pool area [m2]; Hv = heat of vaporization [J/kg]; Cp = liquid heat capacity [J/kg.K];Tb = boiling temperature [K]; and Ta = ambient temperature [K]; and q = radiation per unit area received by the receptor [kW/m2].
Similarly, by combining the Equations 1 and 6, the Equation for distance from point source to receptor becomes:
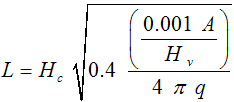 (11)
(11)
where L = distance from Pool Fire center to the receptor [m]; Hc = heat of combustion [J/kg]; A = pool area [m2]; Hv = heat of vaporization [J/kg]; and q = radiation per unit area received by the receptor [kW/m2].
Distance from the Pool Fire center to the receptor:
![]() (12)
(12)
where X = distance from the Pool Fire center projection to the ground to the receptor [m]; L = distance from Pool Fire center to the receptor [m]; and H = height of the Pool Fire center from the ground [m].
Below are relationships reported without for the calculation of Pool Fire exposure time.
![]() (13)
(13)
where Dr = dose receive during the reaction time [(W/m2)4/3.s]; q0 = radiation per unit area received by the receptor during the reaction time [W/m2]; and tr = reaction time (5s).
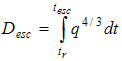 (14)
(14)
where Desc = dose receive during the escape time [(W/m2)4/3.s]; q = radiation per unit area received by the receptor during the escape time [W/m2]; and tesc = escape time (time to reach the radiation intensity level below the dangerous level 1.7 kW/m2).
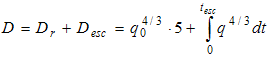 (15)
(15)
where D = total dose of radiation received during exposure [(W/m2)4/3.s]; Dr = dose receive during the reaction time [(W/m2)4/3.s]; q0 = radiation per unit area received by the receptor during the reaction time [W/m2]; tr = reaction time (5s); Desc = dose receive during the escape time [(W/m2)4/3.s]; q = radiation per unit area received by the receptor during the escape time[W/m2]; and tesc = escape time [s].
![]() (16)
(16)
where q = radiation per unit area received by the receptor [W/m2]; A* = parameter calculated from the fit of the model values [-]; x = distance from radiation source to receptor [m]; and a = parameter calculated from the fit [-].
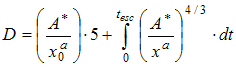 (17)
(17)
where D = total dose of radiation received during exposure [(W/m2)4/3.s]; A* = parameter calculated from the fit [-]; x = distance from radiation source to receptor (it is assumed that person, at the beginning of the fire, is located at a distance of x0 from the fire.) [m]; and a = parameter calculated from the fit [-]; and tesc = escape time [s].
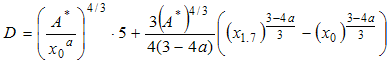 (18)
(18)
where D = total dose of radiation received during exposure [(W/m2)4/3.s]; x = distance from the center of the radiation source to receptor [m]; a = parameter calculated from the fit [-]; and tesc = escape time [-].
Results of calculations
In presented calculations all the calculated heat fluxes correspond to the external emergency zone distances according to the consequence based approach correspond to pre-defined health damage thresholds, i.e. third degree of burns corresponding to the calculated total dose of radiation received during exposure 420 (kW/m2)4/3.s. For the comparison the INERIS study from 1994 have been chosen. Four heat flux values according to four experimental distances for the different amount of the ethanol Pool Fire scenario have been derived.
|
Distance [m] |
Experimental | Calculated | |
|
Heat flux1 [kW/m2] |
Heat flux without τ [kW/m2] |
Heat flux with τ [kW/m2] |
|
| 20 | 1 | 1.5 | 1.2 |
| 15 | 1.6 | 2.3 | 1.95 |
| 10 | 3.1 | 3.8 | 3.3 |
| 5 | 7.8 | 7.2 | 6.5 |
Table 1: Comparison of Pool fire experimental simulation by INERIS with different model.
1 chemical name = ethanol; V = 5 m3; total dose of radiation received during exposure = 420 (kW/m2)4/3.s
From Table 1 two trends could be recognized if compared heat flux from Pool Fire with and without the atmospheric transmissivity parameter. In particular, the distance from approximately 3 m to approximately 7 m underestimate the experimental results. Moreover, the calculated heat flux with atmospheric transmissivity parameter is closer to the experimental results in comparison with the calculated results without the atmospheric transmissivity parameter. Interestingly, the trend changed for the distances approximately higher than 7 m.
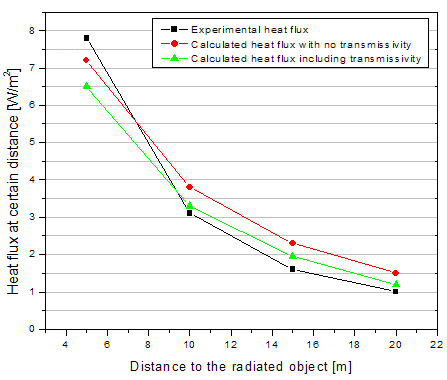
Figure 1: The comparison of the experimental and calculated data.
From the figure it is possible to recognize that presented model is clearly an approximation, but in view of the simplicity of the related computation it has some value in providing an order-of-magnitude estimate. In the near-field, levels of radiation are lower than those experimentally determined. In the far field, predictions of heat fluxes are higher than the experimental values presented with the meaning of conservative approach.
Conclusion
In this paper modified point source model of thermal radiation from Pool Fire has been considered as aids in layout and in preparation of emergency plans. For a variety of reasons this model does not generate the separation distances that are in total agreement and these predicted values are at variance with values set down in codes and standards. The model and adaptations of this model has been run in order to generate comparative design information. The principal geometrical quantities that characterize the Pool Fire in this contribution are the length, the burning rate and the pool diameter. The flame length is only function of the burning rate, density and of the flame diameter. In this study, the comparison of adopted point source model with the pool fire experiments are performed in a calm environment (without wind) so the flame tilt will not be investigated here. On the other end, the radiation emitted by the flame is also analyzed as a function of the heat received by the observer, of the heat of combustion multiplied by the burning rate. This heat flux from Pool Fire decreases with the square of the distance from the source and with the transmissivity of the ambient air. Finally the results are compared using the model with and without the implementation of atmospheric transmissivity in order to approximately quantify its influence on average heat flux measured. Some methods of calculating radiation flux from large fires take into account the “tilting” of the fire due to the wind. Essentially, a more complicated calculation of the view factor from a tilted plate or cylinder is performed. The results are only marginally different than those obtained for vertical plates and cylinders when the target is beyond a few fire diameters away. The difference in results is well within the factor of safety inherent in the calculation procedure resulting from the conservative estimates of the principal parameters. For liquid fuel fires, however, the point source model may be too conservative because these fires are more predictable and there is much more experimental data available to validate a more detailed model.
Acknowledgement
The contribution was prepared in the frame of following projects:
- Opportunity for young researchers, reg. no. CZ.1.07/2.3.00/30.0016,supported by Operational Programme Education for Competitiveness and co-financed by the European Social Fund and the state budget of the Czech Republic.
- Optimization of emergency planning zone and emergency plans creation based on harmful effects of dangerous chemicals released during major accidents with respect to improvement of civil protection reg. no. VG20112013069, supported by Ministry of Interior of the Czech Republic.
- Innovation for Efficiency and Environment, reg. no. CZ.1.05/2.1.00/01.0036 supported by Operation Programme Research and development for Innovation and financed by the Ministry of Education, Youth and Sports.
Literature
[1] BABRAUSKAS, V. Estimating large pool fire burning rate. Fire Technology, 1983, vol. 19, no. 4, pp. 251-261.
[2] BABRAUSKAS, V. Heat Release Rate : SFPE Handbook of Fire Protection Engineering. 3rd ed. Quincy : National Fire Protection Association, Section 3, 2002. Pp. 3-1 to 3-37.
[3] DAYAN, A.; TIEN, C. L. Radiant heating from a cylindrical fire column. Combustion Science and Tech., 1974, vol. 9, no. 1, pp. 41-47.
[4] MUNOZ, J. …[et al.]. Analysis of geometric and radiative characteristics of hydrocarbon pool fires. Combustion and Flame, 2004, vol. 139, pp. 263-277.
[5] FU, T. T. Heat radiation from fires of aviation fuels. Fire Technology, 1974, vol. 10, no. 1, pp. 54-67.
[6] MAY, W. G.; McQUEEN, W. Radiation from large liquefied natural gas fires. Combustion Science and Technology, 1973, vol. 7, no. 2, pp 51-56.
[7] COWLEY, L. T.; JOHNSON, A. D. Oil and Gas Fires : Characteristics and Impact, Offshore Technology Information : Report No. 596, 1992. The Steel Construction Institute. Risk Management Program Guidance for Offsite Consequence Analysis : Appendix C : Flammable Substances, 1999.
[8] US EPA. Risk Management Program Guidance for Offsite Consequence Analysis. Appendix C : Flammable Substances. US EPA, 1999.
[9] TNO Bureau for Industrial Safety. Netherlands Organization for Applied Scientific Research. Methods for the Calculation of the Physical Effects. Hague : Committee for the Prevention of Disasters, 1997.
[10] TNO Bureau for Industrial Safety. Netherlands Organization for Applied Scientific Research. Methods for the Determination of Possible Damage. Hague : Committee for the Prevention of Disasters, 1992.
Vzorová citace
SKŘÍNSKÝ, Jan …[et al.]. Description of Physical-Chemical Parameters of Pool-fire. Časopis výzkumu a aplikací v profesionální bezpečnosti [online], 2013, roč. 6, č. 3-4. Dostupný z WWW: <http://www.bozpinfo.cz/josra/josra-03-04-2013/pool-fire.html>. ISSN 1803-3687.
Užitečné odkazy
Provozovatel portálu
Jeruzalémská 1283/9
110 00 Praha 1


