Calculation method for emergency planning zone used in Spain
METODA VÝPOČTU PRO ZÓNU HAVARIJNÍHO PLÁNOVÁNÍ POUŽÍVANÁ VE ŠPANĚLSKU
Jan Skřínský1, Vilém Sluka2, Martina Pražáková3, Stanislav Malý4
1Energy Research Centre, VŠB - TU Ostrava, 17. listopadu 15/2172, 70833 Ostrava, Czech Republic, jan.skrinsky@vsb.cz
2Department of Major Accidents Prevention, Occupational Safety Research Institute, Jeruzalémská 9, 116 52, Prague, Czech Republic, sluka@vubp-praha.cz
3Department of Major Accidents Prevention, Occupational Safety Research Institute, Jeruzalémská 9, 116 52, Prague, Czech Republic, prazakova@vubp-praha.cz
4Stanislav Malý, RNDr., Department of Major Accidents Prevention, Occupational Safety Research Institute, Jeruzalémská 9, 116 52, Prague, Czech Republic, malys@vubp-praha.cz
Abstract
The goals of this contribution are (i) to summarize the adopted threshold damage criteria used for major accident consequence modeling of fire accidents in Spain and (ii) to numerically compare obtained results with the index-based method used in the Czech Republic. The main objective is to compare complexity of the evaluation of selected European methodologies as far as their application in the case of the same effect and damage model of dangerous flammable substance release, and point out the need to assess the risks from the perspective of emergency planning.
Keywords: Emergency Planning Zone; Fire Accidents Effects and Consequences
Abstrakt
Cílem tohoto příspěvku je (i) shrnout přijatá prahová kritéria poškození používaná pro modelování následků závažných havárií při požárech ve Španělsku a (ii) numericky porovnat získané výsledky s indexovou metodou používanou v České republice. Hlavním cílem je porovnat komplexnost hodnocení vybraných evropských metodik, pokud jde o jejich aplikaci v případě stejného modelu následků a škod při úniku nebezpečné hořlavé látky, a poukázat na potřebu hodnocení rizik z hlediska havarijního plánování.
Klíčová slova: zóna havarijního plánování, účinky a následky požárních havárií
Introduction and interest
It has been well established that the ability to predict the effects of a fire is highly useful for applying preventive measures. Experience shows that one of the preventive tools is external emergency zone. In order to establish the external emergency zone, it is necessary to know the effects of different kinds of accidents. The research in the last decade has resulted in the development of numerous fire consequence models varying from simple empirical models to highly complex computational fluid dynamics models. Mathematical modeling is used as a useful tool to predict the effects and consequences for the thermal radiation that will reach a given target located at a certain distance from the flames. Apart from sophisticated mathematical models, the index-based exists. These methods are based on the classification of hazardous activities in the area of interest by way of categorizing consequences of occurrence of major accidents. The categorization of consequences leads the user to calculate approximately the number of fatalities caused by an accident in a fixed installation with hazardous materials. The main interest of the contribution is the comparison of mathematical-physical method used in Spain with the index-based method used in the Czech Republic from the point of view of fire accident consequences for selected flammable chemical substances and accident scenarios. The reason for the analysis is the knowledge that the more mechanical application of methodological procedure could lead to underestimation or, on the other hand, overestimation of given risks with regard to the surrounding population.
Previous studies
Member States of the European Union use various methods to model effects and damages of major accidents with respect to major accident hazards which are in detail published in (Kirchsteiger et al., 1998). In Spain the risk analysis approach as well as related criteria is defined. From the methodological point of view, Spain adopted "consequence oriented" approach for risk assessment, and use principally different methods and endpoint values than the methodology in the Czech Republic. Therefore, the numerical comparison of emergency planning zone distances seems to be an interesting topic. However, such comparison is not sufficient without analysis.
Analysis
For the evaluation of the zone distances of pool-fire directly from the pool area of flammable liquid we used the simple point source model described by Equations 1-5 (see TNO, 1997; US EPA 1999 and Casal, 2008).
![]() (1)
(1)
where q = radiation per unit area received by the receptor; f = fraction of heat of combustion radiated; m = rate of combustion; Hc = heat of combustion; τa = atmospheric transmissivity; and x = distance from point source to receptor.
![]() (2)
(2)
where m = rate of combustion; Hc = heat of combustion; A = pool area; Hv = heat of vaporization; Cp = liquid heat capacity; Tb = boiling temperature; and Ta = ambient temperature.
![]() (3)
(3)
where m = rate of combustion; Hc = heat of combustion; A = pool area and Hv = heat of vaporization.
The empirical Equation 2 is used for estimating the combustion rate of a flammable substance with a boiling point above the ambient temperature, while the Equation 3 is used for the flammable substance with a boiling point below the ambient temperature. Combining Equations 1 and 2, gives the following Equation for liquid pools of substances with boiling points above ambient temperature:
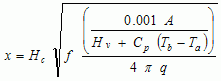 (4)
(4)
where x = distance from point source to receptor; Hc = heat of combustion; A = pool area; Hv = heat of vaporization; Cp = liquid heat capacity; Tb = boiling temperature; Ta = ambient temperature and q = radiation per unit area received by the receptor.
Similarly, by combining the Equations 1 and 3, the Equation for distance from point source to receptor becomes:
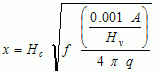 (5)
(5)
where x = distance from point source to receptor; Hc = heat of combustion; A = pool area; Hv = heat of vaporization and q = radiation per unit area received by the receptor.
For the evaluation of the exposure duration for both fireball and pool-fire model we used relationships, which are given in (TNO, 1992):
![]() (6)
(6)
where q = radiation per unit area received by the receptor; A* = parameter calculated from the fit (see Figure 2); x = distance from radiation source to receptor; and a = parameter calculated from the fit (see Figure 2).
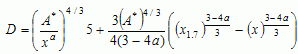 (7)
(7)
where D = total dose of radiation received during exposure; A* = parameter calculated from the fit (see Figure 2); x = distance from the center of the radiation source to receptor; x1.7 = distance from the center of the radiation source to receptor (radiation intensity level below the dangerous level 1.7 kW/m2); and a = parameter calculated from the fit (see Figure 2).
For the evaluation of the zone distances of fireball directly from the mass of flammable liquid in fireball we used the simple point source models described by Equations 8-9 (TNO, 1997 and Casal, 2008).
![]() (8)
(8)
where q = radiation per unit area received by the receptor; τa = atmospheric transmissivity; R = radiative fraction of heat of combustion; Hc = heat of combustion; mf = mass of fuel in the fireball; and L = distance from fireball center to the receptor.
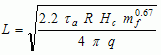 (9)
(9)
where L = distance from fireball center to the receptor; q = radiation per unit area received by the receptor; τa = atmospheric transmissivity; R = radiative fraction of heat of combustion; Hc = heat of combustion; and mf = mass of fuel in the fireball.
For the evaluation of the exposure duration for fireball model we used relationships, which are given in (TNO, 1992):
The Equation 10 for fireball duration normally has the following form, which relates the duration or lifetime of the fireball to the mass of fuel involved in the fireball:
![]() (10)
(10)
where t = fireball duration; k, n = constants; and mf = mass of fuel in the fireball.
In published models, values of the constants k and n range from 0.23 to 2.61, and from 0.0966 to 0.333, respectively. The (TNO, 1997) version of this equation used in this article is as follows:
![]() (11)
(11)
Modeling of the damages
The damages caused by the thermal radiation are proportional to radiation intensity to the four-thirds power times time of exposure (TNO, 1992):
![]() (12)
(12)
where D = thermal radiation dose; t = duration of exposure; and q = radiation per unit area received by the receptor.
The probit functions for the thermal “dose” that could cause the first-degree burns:
![]() (13)
(13)
The probit functions for the thermal “dose” that could cause the second-degree burns:
![]() (14)
(14)
The probit functions for the thermal “dose” that could cause the third-degree burns:
![]() (15)
(15)
where P = probit function; t = duration of exposure; and q = radiation per unit area received by the receptor.
For estimating the distance from a pool-fire or fireball at which a receptor might receive thermal radiation to cause first- and second-degree burns as defined in the case of Spanish approach (Guía técnica, 2002), are the probit above (Equations 13 and 14) substituted into the Equations 1 and 8 that leads to Figure 1.
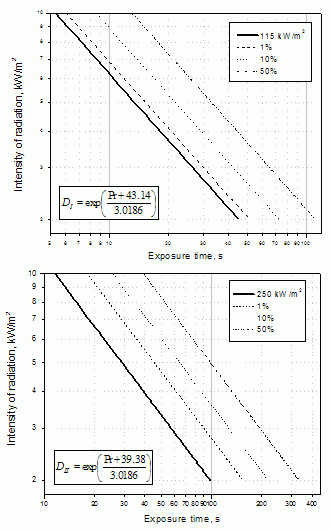
Figure 1: The incident radiation intensity as a function of exposure time for 115 and 250 (kW/m2)4/3.s: (1) “zero damages” zone threshold (bold line), (2) 1% damages (dash line), (3) 10% damages (dot line), and 50% damages (dash double dot line)
Analysis
Up to now the control of emergency planning in Spain is covered by empirical and semi-empirical mathematical models. The endpoint values used for major accident effect and damage modeling of fire accidents in Spain are summarized in Tables 1-2 (Guía técnica, 2002).
| Intervention zone | |||||
| Heat flux [ kW/m2 ] | 7 | 6 | 5 | 4 | 3 |
| Exposition times [s] | 20 | 25 | 30 | 40 | 60 |
Table 1: Endpoint threshold values adopted for intervention zone
| Alert zone | |||||
| Heat flux [ kW/m2 ] | 6 | 5 | 4 | 3 | 2 |
| Exposition times [s] | 11 | 15 | 20 | 30 | 45 |
Table 2: Endpoint threshold values adopted for alert zone
If we transform the endpoint values from tables 1-2 to thermal radiation “dose” values we will receive 250 (kW/m2)4/3.s for the intervention zone and 115 (kW/m2)4/3.s for the alert zone that are values equal to that described in Figure 1.
Spanish examples calculated by Effect 9.0: high of the receiver: 1.7 m, ambient temperature: 15 °C, ambient relative humidity: 70%, amount of CO2 in atmosphere: 0.03%, 1) substance: n-butanol, temperature of the pool: 15 °C, amount: 600,000 kg, pool surface: 314 m2 (diameter: 20 m) and 2) substance: propane, amount: 30,000 kg, initial temperature in vessel: 50 °C, burst pressure vessel: 5.1 bar.
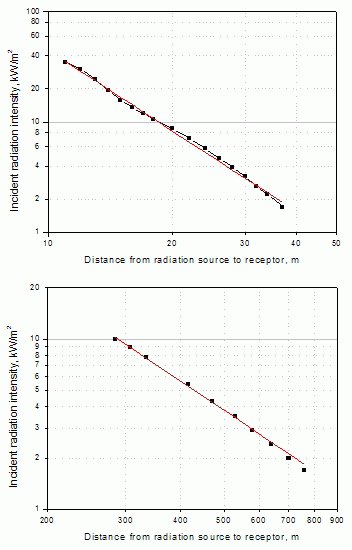
Figure 2: The incident radiation intensity as a function of distance for a 1) pool-fire scenario (n-butane, 600,000 kg) and 2) fireball scenario (propane, 30,000 kg)
Figure 2 shows the decreasing trend of calculated incident radiation intensity for pool-fire for 20 m distance interval. The radiation intensity versus distance relationship is used for calculating the final dependence using the Equation 16 in which the A* and a parameters are obtained from the fit:
![]() (16)
(16)
where q = radiation per unit area received by the re-ceptor; x = distance from radiation source to receptor.
The empirical Equations 7 and 16 are used for estimating zone distances for the pool-fire scenario:
![]() (17)
(17)
Substituting the appropriate values for third-, second- and first-degree burns as 365, 250, and 115 (kW/m2)4/3.s for dose to Equation 17 yields the zone distances in Table 3:
|
Heat flux kW/m2 |
Exposition* s |
Dose (kW/m2)4/3.s |
Distance m |
| 13.6 | 11.2 | 365** | 15 |
| 11.0 | 10.2 | 250*** | 17 |
| 6.6 | 9.2 | 115*** | 22 |
Table 3. Calculated zone distances
*Exposition calculated as t = tesc+ tr = (x1.7 – x0)/u + 5, where tesc = escape time, tr = reaction time 5s, and u = escape speed; **Endpoint values for third-degree burns; ***Endpoint values adopted in Spain.
Figure 2 shows the decreasing trend of calculated incident radiation intensity for fireball for 500 m distance interval. The radiation intensity versus distance relationship is used for calculating the final dependence using the Equation 12 in which for q is substituted Equation 6 and the A* and a parameters are obtained from the fit:
![]() (18)
(18)
where q = radiation per unit area received by the re-ceptor; x = distance from radiation source to receptor.
![]() (19)
(19)
Substituting the appropriate value 12.0 s for the duration time and values 365, 250, and 115 (kW/m2)4/3.s for dose yields the zone distances in Table 4:
|
Heat flux kW/m2 |
Duration s |
Dose (kW/m2)4/3.s |
Distance m |
| 12.6 | 12.4* | 365** | 242 |
| 9.5 | 12.4* | 250*** | 294 |
| 5.3 | 12.4* | 115*** | 420 |
Table 4. Calculated zone distances
*t = 0.852 mf 0.26 (TNO, 1997); **Endpoint values for third-degree burns; ***Endpoint values adopted in Spain.
Results and discussion
From the results of presented models (see Equations 1-15) it was possible to define hazardous areas in which defined pool-fire and fire-ball damages might occur.
Effect distance calculations for the pool-fire scenario
Various distances for the different pool surface diameters of the n-butanol pool-fire scenario, have been observed in the mass range from 600 to 10,000 tons. Zone distances were estimated how by index-based thus by semi-empirical method and calculation. Altogether, sixteen distances were derived and subjected to further analyses. Four distances owing to the non-resolved legally stated indexes and twelve distances owing to the mathematically and physically resolved semi-empirical equations. A global least square analysis of the calculated incident radiation intensity-distance relationship was conducted to the latter one and led to the determination of dose-distance relationship (see Figure 2 and Equations 16-17). The results of the estimation are summarized in Table 5.
|
Amount [t] |
n-butanol [m] |
|||
| Czech | Spain* | Calculation** | ||
| 1 | 2 | |||
| 600 | 50 | 27 | 32 | 33 |
| 3000 | 100 | 48 | 55 | 67 |
| 7500 | 100 | 72 | 81 | 101 |
| >10,000 | 200 | >95 | >105 | >134 |
Table 5: Zone distances in m
* diameters D = 20 m (600t), 40 m (3000t), 60 m (7500t), and 80 m (>10,000t); **1% fatality
All the external emergency zone distances according to the consequence based approach correspond to pre-defined health effect (degree of burns) thresholds. In Table 5 two zones could be recognized: An internal zone, corresponding to the beginning of “lethal” effects, and external zone, corresponding to the beginning of the “irreversible” effects. Apart from these tabulated values, the comparison of the resulted trends (and their classification) is of importance since they are widely used in a variety of industrial land-use and safety distance like application. Figure 3 compares the different zone distances as deriving from the reported Table 5.
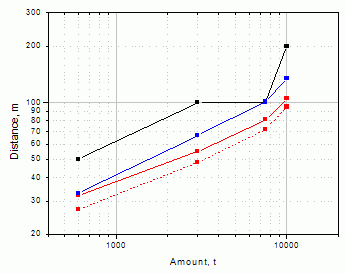
Figure 3: Emergency zone distances for the pool-fire of n-butanol: in the Czech Republic (black), in Spain (red) and calculated (blue)
Effect distance calculations for the fireball scenario
Thirty distances for the different amount of the propane fireball scenario, have been derived in the mass range from 3 to 600 tons. As in the case of pool-fire scenario, zone distances were estimated how by index-based thus by semi-empirical methods as well as calculated by simple point-source model described by Equations 8-9. All the estimated distances are summarized in Table 6 and classified as individual zones according to states.
|
Amount [t] |
propane [m] |
|||
| Czech | Spain | Calculation** | ||
| 1 | 2 | |||
| 3 | 100 | 87 | 137 | 174 |
| 7,5 | 200 | 145 | 154 | 287 |
| 30 | 200 | 294 | 420 | 377 |
| 125 | 400 | 594 | 820 | 738 |
| 600 | 1000 | 1244 | 1690* | 1248 |
Table 6: Zone distances in m
* for t > 20s is D = I4/3·20; **for 1% fatality
From Table 6, in Spain two zones could be recognized as in the case of pool-fire. In contrast with Table 5 starting from the amount of approximately 10 tons a progressive change occurs between the determined Czech and Spanish zone distances. In particular, the distance value 200 m is equal for the 7.5 and 30 tons according to Czech approach, while in adverse to that relation Spanish distance grow up from 145 to 294 m, and from 154 to 420 m, respectively. Moreover, similar trend could be recognized for the distances estimated by semi-empirical mathematical and physical models described by the Equation 9. For these reason, it could be interesting to analyze both trends in detail in terms of graphical interpretation.
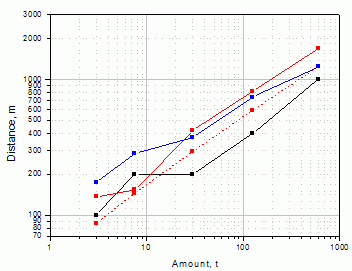
Figure 4: Emergency zone distances for the fireball of propane: in the Czech Republic (black), in Spain (red) and calculated (blue)
Figure 4 compares the different zone distances estimated by semi-empirical mathematical models values for the fireball scenario. The systematic comparison in Figure 4 shows the similar trend between the derived Spanish and calculated values and resolves the further “anomaly” - for the 7.5 tons is the Spanish zone distance almost equal that differs from the trend of equal spacing in the logarithmic scale shown in Figure 4.
Summary and conclusion
The present investigation has started the series of studies for “consequence-based” approach. This approach is based on the assessment of consequences of credible (or conceivable) accidents, without explicitly quantifying the likelihood of these accidents. The difference between two various “consequence-oriented” approaches have been shown on numerical examples. The non-index based semi-empirical model approach in Spanish example and the index-based Czech approaches were demonstrated in terms of external emergency zone distances. This analysis might be used both to evaluate the purpose of the emergency planning zone, and to comparatively evaluate the criteria proposed for calculation of emergency planning zone distances. Individual steps of the presented emergency planning methodology together with the two sets of calculated zone distances were derived, and two applications for the pool-fire and fireball illustrated.
This benchmark study shows that the methods to determine external emergency zone distances used in Czech and Spain are very different. Not only the principle of the methods (index-based vs mathematical-physical) and the guide values differ, but also the effect calculations with their endpoint values (thresholds) vary. In order to understand the differences in detail and to improve the foundations and the value of the risk assessment methodologies, further international sharing of insights and methods is desirable. Although, no explanation was found for the trend described in Figure 4, the values are consistent with each other and seem to be typical for fireball-type of propane. Therefore it could be interesting, as in the case of pool-fire scenario, to make further studies for dangerous substances that could lead to fireball scenario, namely butane, propene and focused on this distance - amount relation.
References
KIRCHSTEIGER, C.; CHRISTOU, M. D.; PAPADAKIS, G. A. Risk Assessment and Management in the Context of the Seveso II Directive Risk Assessment and Management in the Context of the Seveso II Directive. Amsterdam : Elsevier, 1998. (Industrial safety series, 6). ISBN 0-444-82881-8.
Guía técnica Zonas de planificación para accidentes graves de tipo térmico: en el ámbito del Real Decreto 1254/99. In: [Seveso II]. 2002.
The Notice no. 103/2006 Coll., from June 1, 2006 in the Collection of Laws of the Czech Republic, Part 36.
CASAL J. Evaluation of the Effects and Consequences of Major Accidents in Industrial Plants. Amsterdam : Elsevier, 1998. (Industrial safety series, 6). ISBN 978-0-444-53081-3
TNO : methods for the calculation of physical effects resulting from releases of hazardous materials (liquids and gases). CPR 14E, Yellow book; Committee for the Prevention of Disasters. 3rd Edition. 1997.
TNO : methods for the determination of possible damage to pe-ople and objects resulting from release of hazardous mate-rials. CPR 14E, Green Book; Committee for the Prevention of Disasters. 1st Edition, 1992.
US EPA. Risk Management Program Guidance for Offsite Consequence Analysis : Appendix C : Flammable Substances. 1999.
Acknowledgment
The article was prepared in the frame of the projects:
- Optimization of emergency planning zone and emergency plans creation based on harmful effects of dangerous chemicals released during major accidents with respect to improvement of civil protection reg. no. VG20112013069, supported by Ministry of Interior of the Czech Republic.
- Opportunity for young researchers, reg. no. CZ.1.07/2.3.00/30.0016, supported by Operational Programme Education for Competitiveness and co-financed by the European Social Fund and the state budget of the Czech Republic.
Vzorová citace
SKŘÍNSKÝ, Jan…[et al.]. Calculation method for emergency planning zone used in Spain. Časopis výzkumu a aplikací v profesionální bezpečnosti [online], 20123, roč. 6, č. 1. Dostupný z WWW: <http://www.bozpinfo.cz/josra/josra-01-2013/vypocetni-metoda.html>. ISSN 1803-3687.
Užitečné odkazy
Provozovatel portálu
Jeruzalémská 1283/9
110 00 Praha 1


