Využití principu minimax v hodnocení rizik

Abstrakt

Cílem příspěvku je prezentovat možné využití teorie her v rámci hodnocení rizik. Prezentace bude konkrétně zaměřena na jednu ze základních rozhodovacích strategií a to na princip minimax. V první části příspěvku jsou uvedeny základní informace o principu minimax. V dalších částech příspěvku bude popsána možná aplikace tohoto principu při hodnocení rizik v procesním průmyslu. Tato aplikace je následně demonstrována na řešeném příkladu. V poslední části příspěvku jsou vypočtené výsledky diskutovány a také uvedeny možné zdroje kritiky využití tohoto principu v hodnocení rizik.

Klíčová slova: procesní průmysl, riziko, rozhodovací proces, teorie her

Abstract

The aim of this paper is to present the possible use of game theory in risk evaluation. The presentation will specifically focus on one of the basic decision-making strategies, namely the minimax principle. In the first part of the paper basic information about the minimax principle is presented. In the next parts of the paper, the possible application of this principle in risk evaluation in the process industry will be described. This application is then demonstrated by solved example. In the last part of the paper the calculated results are discussed and also possible sources of criticism of the use of this principle in risk evaluation are given.

Keywords: process industry, risk, decision-making process, game

1. Úvod

Princip minimax je v teorii her jednou ze základních strategií pro konfliktní rozhodování pro dva hráče za neurčitosti. Pro účely rozhodovacích procesů v rámci hodnocení rizik lze identifikovat hráče následujícím způsobem. Prvním hráčem je rozhodovatel, druhým hráčem může být například „přírodní událost“, „náhodná situace“, apod. První hráč je považován za hráče inteligentního. U druhého hráče předpokládáme, že jeho tahy jsou náhodné a nesledují žádný cíl. Tohoto hráče lze tedy ve smyslu teorie her považovat za neinteligentního. Zároveň předpokládáme, že první hráč nezná rozložení pravděpodobnosti, kdy například nějaká vybraná extrémní přírodní událost či náhodná situace nastane. V takovém případě se jedná o konfliktní rozhodování za neurčitosti (viz Maňas, 1974).

Mimo strategii minimax lze pro konfliktní rozhodování za neurčitosti uvést další základní strategie: princip nedostatečné evidence, princip minimaxu ztráty a princip ukazatele optimismu (Maňas, 1974).

V případě principu nedostatečné evidence se první účastník chová tak (volí takovou strategii), že všechny možnosti jsou stejně pravděpodobné (druhý neinteligentní hráč volí všechny strategie se stejnou pravděpodobností). V případě principu minimaxu ztráty první účastník volí takovou strategii, která ho zajišťuje proti velkým ztrátám ve srovnání s rozhodnutím, který by provedl v případě znalosti strategie druhého účastníka. Princip ukazatele optimismu princip předpokládá stanovení konstanty (určité míry optimismu), strategie se volí na základě této konstanty (Maňas, 1974). Princip minimax je považován za strategii pesimistického hráče. Při volbě tohoto principu předpokládám maximální ztráty a volím takovou strategii, kde ztráty jsou minimální.

Je zjevné, že volba jednotlivých strategií vede k různým (někdy i výrazně odlišným) výsledkům. Příspěvek se bude věnovat dále pouze principu minimax a to především kvůli jeho zvláštnímu postavení v oblasti hodnocení rizik v procesním průmyslu.

2. Aplikace principu minimax

Při hodnocení rizik je nutné provést rozhodnutí o tom, zda riziko, které posuzuji, je přijatelné či nikoli. Jedná se o konfliktní rozhodování za neurčitosti a v takovém případě mohu podle teorie her použít princip minimax.

Tento princip je využíván například v případě rozhodování o přijatelnosti společenského rizika s využitím kritéria přijatelnosti prezentovaného pomocí linie F-N (Evans a Verlander, 1997).

Pro další vysvětlení souvislosti principu minimax a linie F-N při rozhodovacích procesech budou ve zkrácené podobě prezentovány myšlenkové postupy autorů Evans a Verlander (1997).

Mějme funkci F(n) představující rozdělení středních hodnot četnosti havárií v závislosti na n úmrtích. Jedná se o tzv. FN křivku. Dále mějme funkci C(n), která představuje kritérium přijatelnosti. V případě použití logaritmického měřítka je riziko přijatelné jen tehdy, když platí následující:

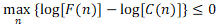(1)

Přičemž n je diskrétní hodnota a platí n > 0 . Po úpravě rovnice (1) můžeme tedy říci, že riziko je přijatelné v případě, když platí:

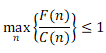(2)

Zaveďme novou veličinu 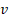 udávající míru, zda je posuzované riziko přijatelné či nikoli. Můžeme potom psát:

(3)

Systém je přijatelný pakliže platí 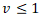. Nyní uvažujme množinu systémů, ze kterých pouze jeden má být vybrán. Rozhodneme, že bude vybrán takový systém, pro nějž hodnota  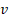bude nejnižší. Pokud systémy mezi nimiž se rozhoduje, budou indexovány pomocí písmene i bude pro toto rozhodnutí platit:

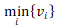(4)

Po dosazení rovnice (3) do výrazu (4) můžeme psát:

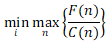(5)

Výraz (5) však reprezentuje rozhodovací pravidlo minimax. Toto pravidlo bude dále prezentováno na konkrétním zjednodušeném příkladu z procesního průmyslu.  

3. Příklad

Ve výrobní společnosti se uvažuje o nákupu výrobní technologie. Rozhoduje se mezi dvěma variantami. První variantu označme i_A, druhou variantu označme i_B. Pro první variantu (i_A) byly stanoveny různé havarijní scénáře s následujícími následky a frekvencemi událostí:

• Pro n₁ = 150 fatálně zraněných platí frekvence události f = 7 · 10^-9 za rok
• Pro n₂ = 100 fatálně zraněných platí frekvence události f = 1,0 · 10^-8 za rok
• Pro n₃ = 5 fatálně zraněných platí frekvence události f = 1,5 · 10^-5 za rok

Pro druhou variantu platí (i_B) platí:

• Pro n₁ = 130 fatálně zraněných platí frekvence události f = 9,2 · 10^-9 za rok
• Pro n₂ = 88 fatálně zraněných platí frekvence události f = 2,5 · 10^-8 za rok
• Pro n₃ = 2 fatálně zraněných platí frekvence události f = 4,1 · 10^-5 za rok

Jakou variantu zvolit? Cena výrobní technologie není rozhodující. Jako rozhodovací strategie bude zvolen princip minimax. Jako kritérium přijatelnosti bude stanoveno nejdříve kritérium přijatelnosti společenského rizika používající se ve Velké Británii v rámci prevence závažné havárie, tj.:

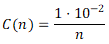(rok^-1) (6)

Aplikujeme výpočetní vztahy (3) a (6). Výsledky výpočtů jsou uvedeny v tabulce 1.

Varianta	Číslo scénáře	C(n) (rok-1)	(-)
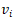iA	1	6,7·10-5	1,1·10-4
	2	1,0·10-4	1,0·10-4
	3	2,0·10-3	7,5·10-3
iB	1	7,7·10-5	1,2·10-4
	2	1,1·10-4	2,2·10-4
	3	5,0·10-3	8,2·10-3

Tabulka 1: Výsledky výpočtu – britské kritérium

Maximální hodnota v v případě varianty i_A je 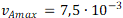, v případě varianty i_B tato hodnota činí 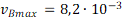. Platí,  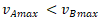Z toho vyplývá, že podle principu minimax je preferována varianta i_A.

Je vhodné si povšimnout, že výsledek rozhodovacího procesu je závislý na zvolených kritériích. Pro srovnání použijme holandské kritérium pro stanovení společenského rizika, které se používá také v České republice tj.:

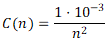(rok^-1) (7)

Aplikujeme výpočetní vztahy (3) a (7). Změna výsledných hodnot je zřejmá z tabulky 2.

Varianta	Číslo scénáře	C(n) (rok-1)	(-)
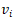iA	1	4,4·10-8	0,16
	2	1,0·10-7	0,1
	3	4,0·10-5	0,38
iB	1	5,9·10-8	0,16
	2	1,3·10-7	0,19
	3	2,5·10-4	0,16

Tabulka 2: Výsledky výpočtu – holandské kritérium

V tomto případě maximální hodnota 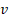 v případě varianty i_A je 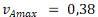, v případě varianty i_B tato hodnota činí 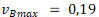. Potom platí 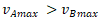. V tomto případě by měla být upřednostněna varianta i_B.

4. Diskuse

Z příkladu je patrné, že volba různých kritérií přijatelnosti vedla k odlišným výsledkům. To bylo ovlivněno především scénářem č. 3 u obou variant. U tohoto scénáře je totiž čtverec počtu obětí v případě použití holandského kritéria u varianty i_A o řád vyšší než u varianty i_B. V případě britského kritéria je však tato změna pouze lineární. Pokud srovnáme výsledné hodnoty 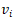 pro holandské a britské kritérium přijatelnosti, je zřejmé, že holandské kritérium přijatelnosti je přísnější než britské (přibližně o 2 až 3 řády).

Během letitého používání principu minimax v oblasti hodnocení rizik byl tento princip podroben také kritice. Jednou z klasických kritik je poukázání na to, že princip minimax je ze své podstaty příliš konzervativní a může vést k rozhodnutím, která se mohou zdát jako nepřiměřená. Další kritika se zaměřuje na nekonzistentnost tohoto přístupu. Příklad nekonzistentnosti je uveden v práci autorů Evans a Verlander (1997). Jiní kritici upozorňují na to, že teorie her obecně byla vybudována pro úzce specifický obor a je problematické měnit doménu (Taleb, 2012).

5. Závěr

V práci bylo prezentováno použití rozhodovacího pravidla minimax při hodnocení rizik s využitím FN křivky. Toto pravidlo bylo demonstrováno na konkrétním příkladu. Hodnocení společenského rizika není však jedinou oblastí, kde je v rámci bezpečnostního inženýrství možné aplikovat princip minimax.

Existují například studie, které se zabývají využitím teorie her pro zvýšení úrovně fyzické ochrany chemických závodů zpracovávající nebezpečné látky. Teorie her se zde využívá pro modelování interakcí mezi „obráncem“ a „útočníkem“. Přičemž „obráncem“ jsou myšleni zástupci chemického podniku a „útočníkem“ teroristické skupiny (Zhang et al., 2021). Jedna z možných strategií v rámci tohoto druhu modelování je také mimo jiné uplatňování principu minimax. Tento princip se podle studie autorů Zhang et al. (2021) ukazuje ve srovnání s jinými ve studii prezentovanými strategiemi jako poměrně robustní.

Pravidlo minimax bylo také použito při návrhu postupu pro hledání odhadů pravděpodobnosti výskytu vzácných událostí (Quigley a Revie, 2011).

Literatura

EVANS, A. W.; VERLANDER, N. Q. 1997. What Is Wrong with Criterion FN-Lines for Judging the Tolerability of Risk? Risk Analysis. 1997, vol. 17, no. 2, s. 157-168. DOI: 10.1111/j.1539-6924.1997.tb00855.x.

MAŇAS, M. 1974. Teorie her a optimální rozhodování. Praha: SNTL, 1974.

QUIGLEY, J.; REVIE, M. 2011. Estimating the Probability of Rare Events: Addressing Zero Failure Data. Risk Analysis. 2011, vol. 31, no. 7. DOI: 10.1111/j.1539-6924.2010.01568.x.

TALEB, N. N. 2012. Antifragile: Things That Gain from Disorder. Penguin Books, 2012. 519 s.

ZHANG, L. …[et al.]. 2021. A chemical plant protection game incorporating bounded rational attackers and distribution-free uncertainties. Journal of Loss Prevention in the Process Industries. 2021, vol. 72, 104545. DOI: 10.1016/j.jlp.2021.104545.

Vzorová citace

TRÁVNÍČEK, Petr; KOTEK, Luboš. Využití principu minimax v hodnocení rizik. Časopis výzkumu a aplikací v profesionální bezpečnosti [online]. 2021, roč. 14, č. 3. Dostupný z: https://www.bozpinfo.cz/josra/vyuziti-principu-minimax-v-hodnoceni-rizik. ISSN 1803-3687.