The optimal (comfortable) operative temperature estimation based on the physiological response of human organism
Stanovení optimálních (komfortních) teplot na základě odezvy lidského organismu
Miloslav V. Jokl1, Karel Kabele2, Stanislav Malý3
1 ČVUT, Fakulta stavební, miloslav.jokl@fsv.cvut.cz
2 ČVUT, Fakulta stavební, kabele@fsv.cvut.cz
3Výzkumný ústav bezpečnosti práce, v.v.i., malys@vubp-praha.cz
Abstract
Problems following the application of optimal operative temperatures estimated on the basis of PMV and the necessity to apply correct values into the new Czech Government Directive No. 523/2002 Code led to experiments based on the physiological human body response instead of on solely man’s feelings in a defined environment. On the basis of experiments on 32 subjects (university students) it has been possible to estimate: a) total balance of hygrothermal flows between the human body and environment, b) the optimal operative temperature as a function of the subject’s activity, c) the thermoregulatory range for each optimal operative temperature, i.e. maximal (category Cmax) limited by the beginnings of sweating, minimal (category Cmin) limited by the beginnings of shivering (category C can be applied to the natural ventilated buildings), optimal (comfort level – category A) defined by time constant 0.368 (can be applied to air conditioned buildings) and submaximum (decreased comfort level – category B) defined by time constant 0.632 (can be applied to buildings with basic air conditioning systems).
Keywords: thermal comfort, hygrothermal microclimate, indoor operative temperature
Abstrakt
Rozpory, ke kterým docházelo při aplikaci optimálních teplot stanovených na základě veličiny PMV, a nutnost stanovení použitelných hodnot pro novelizaci vládního nařízení ČR č. 523/2002 Sb. vedly k experimentální práci, jež se místo pocitů člověka opírá o fyziologickou odezvu organismu na exponující stav prostředí. Pokusy na 32 subjektech (univerzitní studenti) umožnily stanovit a) celkovou bilanci tepelně-vlhkostních toků subjektů, b) závislost optimální operativní teploty na aktivitě subjektu, c) termoregulační rozmezí pro každou optimální teplotu, a to maximální (kategorie Cmax), omezenou počátky pocení, minimální (kategorie Cmin), omezenou počátky třesu, (aplikovatelné na budovy s přirozeným větráním), optimální (úroveň komfortu – kategorie A), určenou časovou konstantou 0,368 (aplikovatelné na budovy s klimatizací) a submaximální (úroveň sníženého komfortu – kategorie B), určené časovou konstantou 0,632 (aplikovatelné na budovy s úsporně provozovanou klimatizaci.
Klíčová slova: tepelný komfort, tepelně-vlhkostní mikroklima,operativní teplota v interiéru
1. Introduction
The provision of optimal hygrothermal conditions, i.e. first of all optimal operative temperature (air being calm and air temperature reaching radiant temperature) is the principal condition for healthy living of a man in building interior. Optimal operative temperature so far is to be calculated from PMV (Predicted Mean Value) (see e.g. EN ISO 7730 Moderate Thermal Environment) estimated on the basis of positive feeling of 80% of present persons. The feelings of a man are very subjective values being impacted by many other factors in addition to hygrothermal conditions, e.g. by indoor interior colors, a man’s mood etc. Furthermore, as a result of the way of experimental estimation of PMV and proved by other experimental works (see Fishman, Pimbert 1979, Newsham, Tiller 1995), it is valid approximately for the neutral zone only. The more leave the neutral zone the more the real values leave the values calculated from PMV, see Fig. 1. And more: the higher man’s activity the higher the difference. The application of high activity values is then impossible in practice. In Fig. 2 the mean thermal sensation vote is plotted against operative temperature for a range of velocities. Each point represents the mean vote of thirty two subjects. The correlation between operative temperature and the mean thermal sensation vote is high with a correlation coefficient of 0.97 (n=5). There is no significant difference between sexes. The solid curve is the regression line for the individual vote (n=80). For comparison, the dotted line represents the results for 172 Japanese subjects in conditions of low air movement reported by Tanabe (1987) and the dashed line represents calculated PMV values.
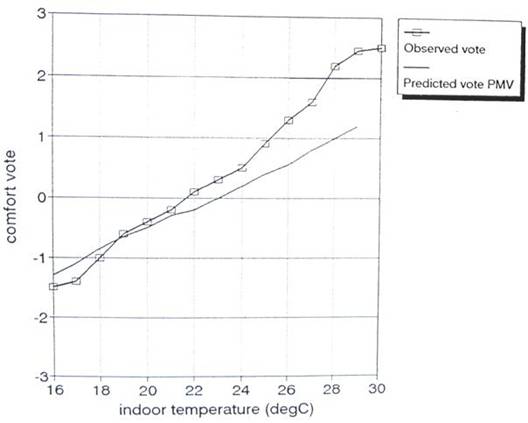
Fig. 1a Comparison of mean thermal comfort votes (ASHRAE scale) with predictions by the PMV model in an English office building (Fishman and Pimbert, 1979). Activity 80 W/m2, clothing 0.64 up to 0.82 clo
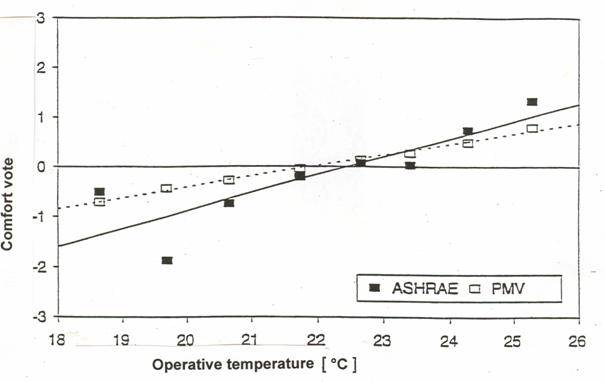
Fig. 1b Comparison of mean thermal comfort votes (ASHRAE scale) with predictions by the PMV model in a building (Newsham and Tiller, 1995). Activity 70 W/m2, clothing 0.78 ± 0.21 clo
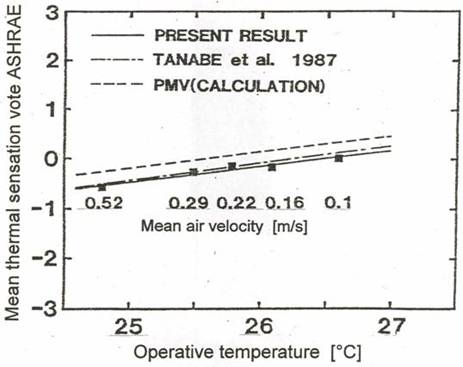
Fig. 2 Mean Thermal Sensation Vote versus Operative Temperature for Japanese College-age Subjects (Tanabe et al. 1987)
Further important results are from research at Reading University (Croome et al.1993) as they take into account the opening and closing of doors, i.e. the ventilation rate, see Fig. 3.
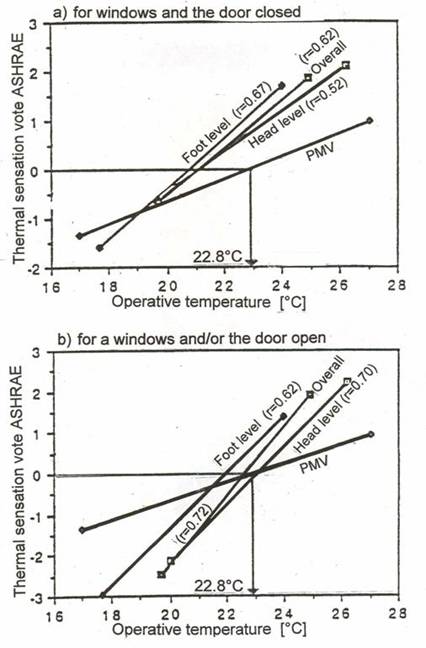
Fig. 3 Effect of operative temperature on thermal sensation vote }Activity 1.2 met, clo value results from neutral temperature 22.8° C, rh=40-55%, mean radiant temperature equals air temperature (Croome et al. 1993)
When the windows and doors were closed, the mean thermal sensation tended to be on the warm side of neutral. When the windows and doors were open, the votes were spread widely over the thermal sensation scale. However, the calculated PMV values corresponding to the tests were close to the neutral point for most of the test conditions. This suggests that, in this investigation, PMV underestimates the thermal impression for the case of the windows and doors shut and undervalues the change in thermal impression for both cases.
This may be due to three main reasons. The first are the assumed steady state laboratory conditions used in the derivation of the PMV equation. The second is the oversimplified approach to the assessment of the metabolic rate of the occupant. The occupants rarely sat in the room for a long period, say one hour, without moving around. The third is the sensitivity of PMV to clo values (Croome et al. 1993). It can be concluded that the PMV equation over predicts the neutral temperature by as much as 2K and under predicts the comfort requirement when air temperature deviates from neutrality.
Humphreys and Nicol (2000) have suggested that there may be formulaic errors in such a complex index as is PMV with two contributing factors:
- Steady state approximation. PMV, as other indices of warmth, is a steady state heat exchange equation and therefore its application to the office environment can only be an approximation. Recent research shows that among office population temperature of fingers varies extensively and rapidly, indicating that the body thermal state of office workers is in continual flux (Humphreys et al. 1999). This suggests that it is better to regard them as being in dynamic thermal equilibrium rather than in a steady thermal state. By extension, the same is likely to be true of other and more varied pursuits. Thus, any index built on steady state assumptions is of limited relevance to normal living. Such indices excluding thermoregulation cannot therefore simulate real life conditions.
- Inaccurate numerical formulae for steady state. The majority of indices have errors in numerical values used in the equations, such as convective and radiant heat transfer coefficients, skin temperature and sweat rates assumed in comfort conditions. These contribute to formulaic errors and additionally there are numerical errors attributable to conceptual simplifications. For example, although the calculation of PMV is based on calculated skin temperature and sweat rate but when considering conditions outside neutral, it is based solely on hypothetical heat load. These results in the same body thermal states being attributed different PMV values in different environments (Humphreys and Nicol 1996). Conceptual and numerical approximations add to formulaic error.
And maybe the most important: from PMV system no thermoregulatory ranges can be estimated.
These are the reasons we decided to estimate optimal operative temperatures on the basis of the physiological response of human organism.
2. Mathematical Model of the Physiological Body response
The total heat rate production and its distribution into individual components during heat exchange between the human body and the environment are shown in Fig. 4, where qm=M-W = metabolic heat (see Jokl 1989). qres and qev,d are the components of the heat rate from the organism by respiration and by skin moistening (evaporation), with the human body being in the thermal neutral zone. The heat flow qdry represents the component transferred from the organism through the clothing layer with a total thermal resistance Rt,wa(qdry= qc+qr). The regulatory process within the neutral zone is achieved mainly by vasodilatation and vasoconstriction changing the body’s internal resistance into the thermoregulatory and adaptational heat flux qtr a qa to the skin surface. qtr a qa is the heat flux regulating the instantaneous value of the skin temperature during the subject’s interaction with environment, qtr is the organism’s immediate response to the changes of the microclimate or metabolic heat changes; qa is the reaction shift due to adaptation to heat in summer and cold in winter. qtr + qa may be negative (heat loss) or positive (heat gain). It is the transient heat flow – even in the thermal neutral zone – that is called “quasi-stationary”, to be differentiated from the hyperthermia and hypothermia zone.
qtr + qa represents the rates of heat storage or heat debt accumulation. When the body is in a steady-state thermal balance with the environment, these therms are equal to zero. But it is possible to consider the state of the subject in the neutral zone by non-steady-state conditions due to periodical changes of metabolic heat rate, qm, or short thermal excitations in time followed by changes of internal thermal resistance of body within the neutral zone.
The temporary characteristics of each non-steady process are determined, in addition to the thermal resistances Rt,i and Rt,wa by the human body heat capacity, Ct. The values characterizing the heat exchange are: Tsk, Tcore and Tg. The internal thermal resistance, Rt,i also determines the changes in thermoregulation and the adaptational heat, qtr + qa, which is necessary for maintaining the skin temperature within physiological values if the core temperature should remain constant (Tcore = 36.7 ± 0.4 °C).
The heat flow balance, as presented in the model shown in Fig. 4 can be expressed by a thermal flux equation at the boundary: subject-environment. Thus (if heat conduction is neglected):
![]() (1)
(1)
where qev=qev,ins +qev,sens= qev,ins+qsw [W.m-2]
qm-qres-qev,ins= qi [W.m-2]
qsw= 0.6(qm-58.14) [W.m-2]
= the quantity of excreted sensible but mostly invisible sweat, it was estimated by weighing during experiments as a mean value for the whole range.
Heat flux within the human body can be represented as (see model in Fig. 4):
![]() (2)
(2)
where Gt,ti is total body thermal conductance, which could be expressed by Equation 3:
![]() [W.m-2.K-1] (3)
[W.m-2.K-1] (3)
where Gt,i is the internal thermal conductance and Gt,m is the metabolic thermal conductance.
The thermoregulation and adaptational heat flux first affects the skin temperature, Tsk. The internal thermal resistance value, Rt,i = 1/ Gt,i, characterizing the vasodilatation and vasoconstriction process, can be calculated from the equation:
![]() (4)
(4)
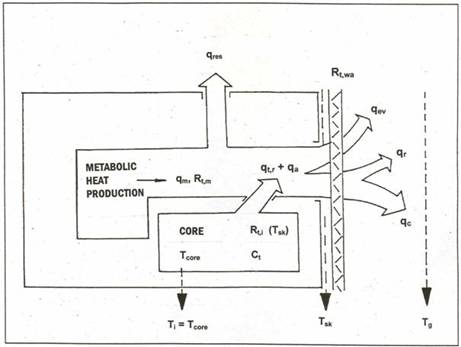
Fig. 4 Total heat rate production and its distribution in individual components during heat exchange between the human body and the environment (qm metabolic heat, qres respiration heat, qtr thermoregulatory heat, qev evaporative heat, qc convective heat, qr radiant heat, Rt,wa total thermal resistance of clothing, Rt total internal thermal body resistance, Ct thermal body capacity, Ti deep body temperature, Tcore core body temperature, Tsk skin temperature, Tg globe temperature
3. Experimental estimation of mathematical model parameters
An experiment lasting several years was undertaken in the climatic chamber from which the parameters in Equation (1) and (4) could be identified.
The experimental subjects were male university students each of them underwent six experiments lasting about three hours at four levels of activity: (1) sitting in a chair, (2) sitting on a bike-ergometer without pedaling, (3) pedaling on a bike-ergometer with a 40 W load and (4) pedaling on a bike-ergometer with a load of 1 W per kg body mass (as long as he was able to do it). Metabolic heat production during each activity was measured by indirect calorimetric method. Mean skin temperature, heat rate and body water loss were estimated continuously during each experiment.
Two sets of clothing were used by the subjects: lightweight (pajamas) and a heavier one (anti-g suit for fighter pilots). The results of anti-g suit experiments will be presented in a separate report.
There were no differences between air temperature and surface wall temperatures – it could be supposed globe temperature equals operative temperature. Six temperatures were chosen (29±3 °C and 14±3 °C, which determine temperature ranges where some of the subjects started to leave the neutral zone and appeared to begin sweating or shivering). The originally chosen range of temperatures 8, 11, 14, 17, 20, 23, 26, 29, 32°C was found not to be necessary and thus they was reduced.
Within the comfort range the relative humidity was maintained corresponding to a partial water vapour pressure from 700 to 1850 Pa. The beginning of sweating and shivering was always assessed by the same person. Experiments were carried out during all seasons, thus reflecting the seasonal adaptation effect on maximal and minimal thermoregulatory heat, i.e. it was possible to determine adaptational heat. But it was evident that it can be neglected (Jokl, Moos 1992) being lower as 0.2 °C (it is within the range of experimental faults of measuring the temperatures). The same finding has been described by other authors (see Fanger 1970). The results were only accepted from subjects within the thermal neutral zone with the thermoregulatory heat constant.
The graph construction of Tg = f(qm)
The measured values are plotted as qdry = f(qi - qsw) in Fig. 5, where for optimal valuesthe linear equation - qdry = qi - qsw [W.m-2] representing equilibrium is valid. The application of this graph into the practice is very difficult; useful is the relationship Tg= f(qm). Therefore the linear relationship from Fig. 5 has been transferred into the graph in Fig. 6 by plotting a regression line through points limited by equation – qdry - (qi - qsw) = ±4.8 [W.m-2] in Fig. 6.
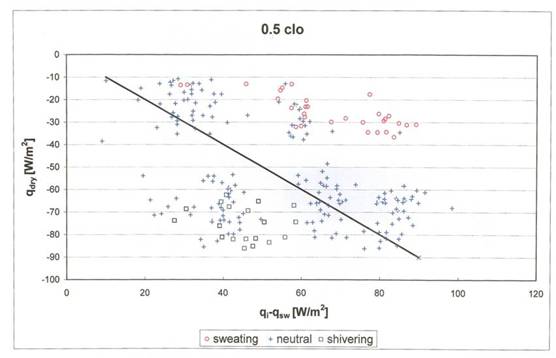
Fig. 5 The graph of the relationship qdry= f(qi - qsw) for clothing 0.5 clo, points from experiment. Optimal values are on the line - qdry = qi – qsw
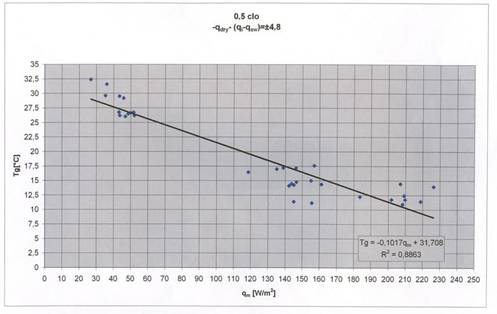
Fig. 6 The graph of the relationship Tg= f(qm) for optimal values transferred from graph on Fig. 3 within the range – qdry – (qi - qsw)= ±4.8, where the value ±4.8 W/m2 represents the minimal thermoregulatory heat
The value of ±4.8 W.m-2 of the regression line is the minimal thermoregulatory heat, i.e. represents maximal vasoconstriction in human body and can be estimated from the minimum value of human body internal thermal conductivity (see Fig. 7) which equals 9.07 W/m2K (for core body temperature Ti= 36.6 °C, skin temperature Tsk= 30.5 °C and qm= 45.7 W/m2).
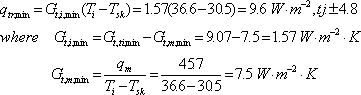
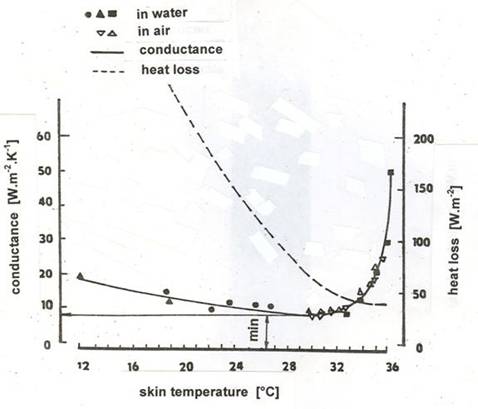
Fig. 7 Human body thermal conductance Gt,ti and human body heat loss as a functionof skin temperature Tsk for resting subject during day (qm=45.6 – 57.4 W.m-2) (Burton, Bazett 1936, Du Bois et al. 1952, Lefevre 1898, Liebmaster 1869) (from Itoh et al. 1972)
The estimation of thermoregulatory range
The widest thermoregulatory range, i.e. from optimum up to the beginning of visible sweating can be estimated by plotting the regression line into the points of beginning of sweating. But for comfort lower values are necessary, without visible sweating occuring. This area is between the line of optimum and the tangent from origin (being an intersection of the line of optimum and the regression line of beginning of sweating) to the area of beginning of shivering (see Fig. 8). These tangents are analogous to the thermoregulatory range of C category according to CR 1752-1998.
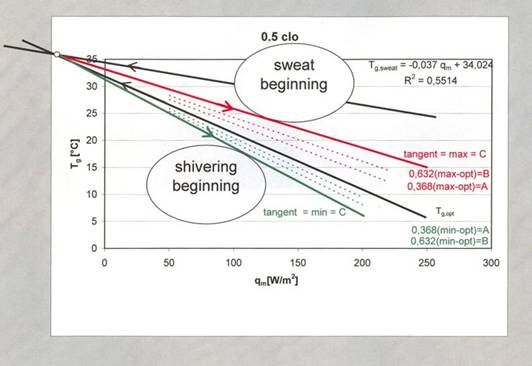
Fig. 8 The way how to get the thermoregulatory ranges. See text for explanation
For A and B categories account must be taken that the human is a thermoregulatory mechanism in the surrounding environment balancing the operative temperature changes by thermoregulatory heat flows in the human body so that an equilibrium can be reached, this at three levels (analogically to technological mechanisms) (see Fig. 9):
- level A, corresponding to the time constant 0.368 DTo,tr,max
- level B, corresponding to the time constant 0.632 DTo,tr,max
- level C, corresponding to the time constant 1.000 DTo,tr,max
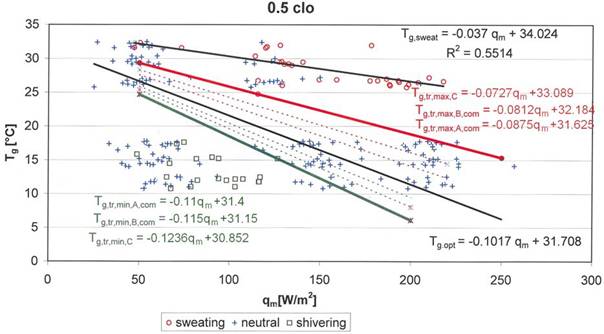
Fig. 9 The graph of the relationship Tg= f(qm) with the regression line of beginnings of sweating and the thermoregulatory range for levels (categories) A, B, C for warm (towards beginnings of sweating) and for cold (towards beginnings of shivering)
Level A is valid for the building interiors with the highest requirements and can only be attained by air conditioning systems application. The level C is valid for the building interiors with the lowest requirements, usually only naturally ventilated. Level B covers the remaining buildings where air conditioning is necessary only in some cases.
The time constant according to control theory characterizes the system response, (human organism response) to the operative temperature changes and equals to the product of system thermal resistance R and its thermal capacity C:
- time constant = R.C
- where R= Rti + Rtwa [W-1.m2.K]
Thermoregulatory changes are shown in Fig. 11 as transferred from Fig. 9 and also rounded up to 0.5 °C for application in practice. For a complete list of values see Table 1.
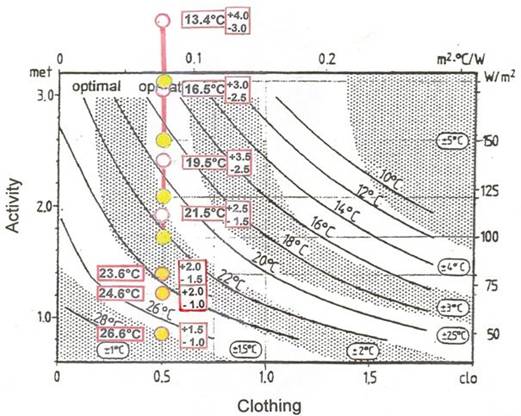
Fig. 11 Comparison of experimentally found optimal operative temperatures with the values in ISO 7730 (presented in graph correspond to temperatures only, not to activity)
| °C | 50 | 70 | 80 |
100 W/m2 |
120 | 150 | 180 |
| sweat | 32.2 | 31.4 | 31.1 | 30.3 | 29.6 | 28.5 | 27.4 |
| sweat -opt | 5.6 | 6.8 | 7.5 | 8.8 | 10.1 | 12 | 14 |
| sweat-opt (0.5) | 5.5 | 6.5 | 7 | 8.5 | 10 | 12 | 13.5 |
| Max | 29.3 | 27.9 | 27.2 | 25.8 | 24.4 | 22.3 | 20.2 |
| max C – opt | 2.7 | 3.4 | 3.7 | 4.3 | 4.9 | 5.9 | 6.8 |
| max C - opt (0.5) | 2.5 | 3 | 3.5 | 4 | 4.5 | 5.5 | 6.5 |
| max B (0.632) | 28.3 | 26.7 | 25.9 | 24.3 | 22.6 | 20.2 | 17.7 |
| max B – opt | 1.7 | 2.1 | 2.3 | 2.7 | 3.1 | 3.7 | 4.3 |
| max B - opt (0.5) | 1.5 | 2 | 2 | 2.5 | 3 | 3.5 | 4 |
| max A (0.368) | 27.6 | 25.8 | 24.9 | 23.1 | 21.3 | 18.6 | 15.9 |
| max A - opt | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.2 | 2.5 |
| max A -opt (0.5) | 1 | 1 | 1 | 1.5 | 1.5 | 2 | 2.5 |
| opt | 26.6 | 24.6 | 23.6 | 21.5 | 19.5 | 16.5 | 13.4 |
| min A(0.368) | 25.9 | 23.7 | 22.6 | 20.4 | 18.2 | 14.9 | 11.6 |
| min A - opt | -0.7 | -0.9 | -1 | -1.1 | -1.3 | -1.5 | -1.8 |
| min A - opt (0.5) | -0.5 | -0.5 | -0.5 | -1 | -1 | -1.5 | -1.5 |
| min B (0.632) | 25.4 | 23.1 | 21.9 | 19.6 | 17.3 | 13.8 | 10.4 |
| min B- opt | -1.2 | -1.5 | -1.6 | -1.9 | -2.2 | -2.6 | -3.1 |
| min B - opt (0.5) | -1 | -1 | -1.5 | -1.5 | -2 | -2.5 | -3 |
| min | 24.7 | 22.2 | 21 | 18.5 | 16 | 12.3 | 8.6 |
| min C - opt | -1.9 | -2.4 | -2.6 | -3 | -3.5 | -4.2 | -4.8 |
| min C - opt (0.5) | -1.5 | -2 | -2.5 | -3 | -3 | -4.0 | -4.5 |
Table 1b Optimal operative temperatures and thermoregulatory range as a function of man’s activity qm
4. A comparison of optimal values and thermoregulatory ranges with accepted values
The proposed optimal temperatures and their thermoregulatory ranges were compared with the values according to ISO 7730 (Moderate thermal environments ISO 7730-1984 (E)), CR (1752) (1998) and ISO/DIS 7730 (2003), ANSI/ASHRAE Standard 55-2004.
The comparison of the above proposed operative temperatures with the values by CR 1752 and ISO/DIS 7730 is presented on Table 2 and on Fig. 11. There is agreement of operative temperatures for 50 W/m2, 70 W/m2 and 80 W/m2. For higher activities the values differ: the higher the activity, the higher the operative temperature difference. There is agreement with experiments (sitting persons in the neutral zone) on which PMV value is based.
The comparison of the proposed optimal operative temperatures with the values according to ISO and ANSI/ASHRAE is presented in Table 3 and Fig. 12. There is an evident agreement for low activities (graph is also based on ISO 7730).
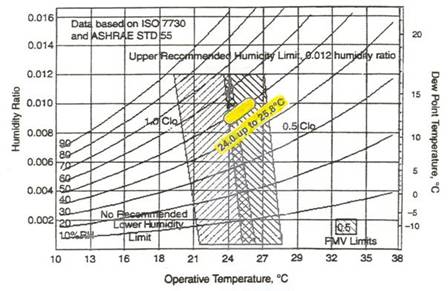
Fig. 12 Comparison of experimentally found optimal operative temperatures with the values in ANSI/ASHRAE
| Category | CR + ISO/DIS | Jo/Ka |
| A (air conditioning) | 24.5 ± 1.0 | 24.6 + 1.0 – 0.5 |
| B (air conditioning and natural ventilation) | 24.5 ± 1.5 | 24.6 + 2.0 – 1.0 |
| C (natural ventilation) | 24.5 ± 2.5 | 24.6 + 3.0 – 2.0 |
Table 2 The comparison of experimentally found operative temperatures with the values in CR 1752 and ISO/DIS 7730 (2003) in categories A, B, C (0.5 clo, 1.2 met)
| qm | [W/m2] | 50 | 70 | 80 | 100 | 120 | 150 | 180 | |||||||
| [met] | 0.86 | 1.20 | 1.38 | 1.72 | 2.07 | 2.59 | 3.10 | ||||||||
| Jo/Ka [°C] (B) | 26.6 | +1.5 | 24.6 | +2.0 | 23.6 | +2.0 | 21.5 | +2.5 | 19.5 | +3.0 | 16.5 | +3.5 | 13.4 | +4.0 | |
| -1.0 | -1.0 | -1.5 | -1.5 | -2.0 | -2.5 | -3.0 | |||||||||
| ISO 7730 (1984) | 26.6±1.5 | 24.5±1.5 | 23.6±2.0 | 22.3±2.0 | 20.6±2.5 | 18.5±2.5 | 16.4±2.5 | ||||||||
| CR 1752, ISO/DIS 7730 (2003) [°C] (B) | - | 24.5±1.5 | 23.5±2.0 | - | - | - | - | ||||||||
| ANSI/ASHRAE 55 (1992)To active= To sedentary – 4.5 (met – 1.2) [°C] | - | 24.5 | 23.7 | 22.2 | 20.6 | 18.2 | 16.0 | ||||||||
Table 3 The comparison of experimentally found operative temperatures with the values in ISO and ANSI/ASHRAE (clothing 0.5) (Remark: (B) means category)
5. Discussion
The optimal operative temperatures derived from PVM values (from the 1970’s) are now not fully acceptable. It is more precise to use optimal operative temperatures based on the physiological human body response and not based on the man’s feelings only. It has been proved by experimental works (Fishman, Pimbert 1979) and shown when ISO values have been applied in practice. The higher the man’s is activity, the higher the discrepancy in the optimal temperature. Because of this discrepancy, the new Czech Government Directive No. 523/2002 Code is based on the presented values and not on ISO/DIS 7730, which is based on PMV. The absence of adaptation to heat and cold, for example resulting from a stay in heated rooms in winter and in air-conditioned cars in summer, in the directive results in the same optimal operative temperatures for winter and for summer; temperatures are differentiated only by various clothing.
6. Results
From the mathematical model (Fig. 4) the role of various heat flows produced by the human body as it interacts with the environment is evident. All the heat flows must be in mutual equilibrium the human body to stay homoiotherm. The application of this graph in practice is very difficult and Tg=f(qm) is a more useful relationship (Fig. 6). This equilibrium is the basis for optimal operative temperature estimation (Fig. 5). The experimental data on the beginning of sweating and the beginning of shivering enable the thermoregulatory ranges to be estimated (Fig. 8). The thermoregulatory area is between the line of optimum and the tangent from pole, defined as the intersection of the line of optimum and the regression line of beginning of sweating, to the field of beginnings of sweating (upper limit, level Cmax) and to the field of beginning of shivering (lower limit, Cmin). It is interesting and in agreement with human feelings, that the thermoregulatory field for cold is smaller than the thermoregulatory field of the warm area – human body is more sensitive to temperature decrease in cold area. The question is how to sub-divide the thermoregulatory range into categories (A, B and C). Instead of qualified assumption, it is proposed to base the categories on control theory. The human body does behave as any other system to which control theory can be applied. It is proposed that human body time constant is used to differentiate the categories. These values were used: time constant 0.368ΔT0,tr,max (A), 0.632 ΔT0,tr,max (B) and 1.0 ΔT0,tr,max, which correspond to categories A, B and C (Fig. 6). Category A can be applied to air conditioned buildings and category C to natural ventilated buildings. As a result, two previously separate methods of assessment can be merged, those for air conditioned buildings, based on PMV, and for natural ventilated buildings, based on a mean monthly outdoor temperature. The results have been compared with the values according to ISO 7730, CR (1752) (1998), ISO/DIS 7730 (2003) (Table 2 and 3) and with ANSI/ASHRAE Standard (Table 3). But, most importantly, it was possible to base the new Czech Government Directive No. 523/2002 Code (Table 3) on the new findings, which were used to derive the compulsory microclimatic condition for workplaces in the Czech Republic.
Acknowledgements
We would like to thank to Professor D.J. Nevrala for help with the English text.
References
1. ANSI/ASHRAE Standard 55-2004. Thermal Environmental Conditions for Human Occupancy.
2. Croome, D.J.; Gan, G.; Abwi, H.B. Evaluation of indoor environment in naturally ventilated offices. In Research on indoor Air Quality and Climate : CIB Proceedings, Publication 163. Rotterdam 1993.
3. EN ISO 7730. Moderate Thermal Environment.
4. European technical report CR 1752-1998 “Ventilation for buildings : Design Criteria for the indoor Environment”.
5. FANGER, P.O. Thermal Comfort. Copenhagen : Danish Technical press, 1970.
6. FISHMAN, D.S.; PIMBERT, S.L. Survey of the objective responses to the thermal environment in offices. In Indoor Climate (eds P.O. Fanger and O. Valbjorn).Copenhagen : Danish Building Research Institute, 1979. S. 677-698.
7. HUMPHREYES, M.A.; NICOL, J.F. Effects of measurement and formulation error on thermal comfort indices in the ASHRAE Database of field studies. ASHRAE Transactions, 2000, no. 106 (2), p. 493-502.
8. HUMPHREYES, M.A., NICOL, J.F. Conflicting criteria for thermal sensation within the Fanger Predicted Mean Vote equation. In CIBSE/ASHRAE Joint National Conference Proceedings : vol. 2. Harrogate, 1996. S. 153-158.
9. HUMPHREYES, M.A., NICOL, J.F. An analysis of some observations of finger-temperature and thermal comfort of office workers. Edinburgh (UK) : Indoor Air, 1999.
10. ITOH, S.; OGATA, K.; YOSHIMURA, H. Advances in Climatic Physiology. Tokyo : Igatu Shion, 1972.
11. JOKL, M.V. Microenvironment : the theory and Practice of Indoor Climate. Illinois : Thomas, 1989.
12. JOKL, M.V.; MOOS, P.; ŠTVERÁK, J. The human thermoregulatory range within the neutral zone. Physiol. Res., 1992, no. 41, s. 227-236.
13. JOKL, M.V.; MOOS, P. Die Warmeregelungsgrenze des Menschen in neutraler Zone. Bauphysik, 1992, 14, s. 175-181.
14. Nařízení vlády č. 523/2002 Sb., kterým se mění nařízení vlády č. 178/2001 Sb., kterým se stanoví podmínky ochrany zaměstnanců při práci (Government Directive No. 523/2002 Code., changing the Government Directive No. 178/2001 Code. prescribing the conditions for employees protection during the work).
15. NEWSHAM, G. R.; TILLER, D. K. A field study of Office Thermal Comfort Using Questionnaire Software. National Research Council Canada, Internal report No. 708, Nov. 1995.
16. TANABE, S.-I.; KIMURA, K.-I.; HARA, T.; AKIMOTO, T. Effects of air movement on thermal comfort in air-conditioned spaces during summer season. Journal of Architecture, Planning and Environmental Engineering, 1987, no. 382, s. 20-30.
Užitečné odkazy
Provozovatel portálu
Jeruzalémská 1283/9
110 00 Praha 1


