Determination of explosion characteristics of fuels/air mixtures - polymonial approximations
oDVOZENÍ VÝBUCHOVÝCH CHARAKTERISTIK PALIVO/VZDUCHOVÝCH SMĚSÍ – POLYNOMIÁLNÍ APROXIMACE
Jérôme Mahin1, Jan Skřínský2
1Département ingénieur industriel, Haute Ecole de Namur-Liège-Luxembourg (HENALLUX), jerome.mahin@gmail.com
2Energy Research Centre, VSB-Technical University of Ostrava, corresponding author: jan.skrinsky@vsb.cz
Abstract
The present work addresses theoretical prediction and experimental determination of explosion characteristics (explosion pressure, maximum explosion pressure, adiabatic explosion pressure). The correlations of experimental data obtained from either from experiment or thermodynamic model are presented. The goal of this article is to show: how the experimental data can be correlated from a uniform point a view through non-dimensionalization, and how the proposed polynomial function can be derived directly from the behavior of dimensionless plots of the experimental data. At the same time, the theoretical study applying on maximum explosion pressure is presented and shows the detail analysis for different input thermodynamic data files. The maximum explosion pressures, computed by assuming chemical equilibrium within the explosion front are examined in comparison with the measured explosion pressures of two gases (CH4 and H2) at atmospheric conditions.
Keywords: Gas explosion, GASEQ 0.79, polynomial approximation, methane, hydrogen
Abstrakt
Presentovaná práce se zabývá teoretickou predikcí a experimentálním stanovením výbuchových charakteristik (výbuchového tlaku, maximálního výbuchového tlaku, adiabatického tlaku výbuchu). Jsou prezentovány korelace dat získaných z experimentu nebo termodynamickým modelem. Cílem tohoto článku je ukázat: jak je možné provést korelaci experimentálních dat i přes bezrozměrnost, a jak lze navrhovaný polynom funkce přímo odvodit od chování bezrozměrných experimentálních dat. Teoretická studie zároveň presentuje použití teoretického výpočtu maximálního adiabatického tlaku výbuchu pro různé vstupní termodynamické datové soubory. Maximální výbuchové tlaky, vypočítané za předpokladu chemická rovnováha v přední části výbuchové vlny jsou zkoumány na příkladu naměřených tlaků výbuchu dvou plynů (CH4 a H2) za atmosférických podmínek.
Klíčová slova: Výbuch plynu, GASEQ 0.79, polynomiální aproximace, metan, vodík
Introduction
Explosions in the process industry cause fewer serious accidents than fire but more than toxic release. When it does occur, however, it often inflicts greater loss of life and damage than fire. Explosion is usually regarded as having a disaster potential greater than that of fire but less than that of toxic release (Lees, 2012). What Is an Explosion? An explosion is an exothermal chemical process that, when occurring at constant volume, gives rise to a sudden and significant pressure rise (Eckhoff, 2005). A confined explosion occurs in a confined space, such as a vessel or a building. The two most common confined explosion scenarios involve explosive vapors and explosive dusts. Empirical studies have shown that the nature of the explosion is a function of several experimentally determined characteristics. These characteristics depend on the explosive material used and include flammability or explosive limits, the rate of pressure rise after the flammable mixture is ignited, and the maximum pressure after ignition. These characteristics are determined using laboratory devices (Crowl and Louvar, 2002). In the present study we have used the 1 m3 explosion apparatus built by OZM Research s.r.o. at Energy Research Centre, VŠB - Technical University of Ostrava.
Numerical method
Thermodynamic model
Computational method used for calculation of adiabatic explosion pressure, Pad, in this study has been adopted by several authors (e.g. Schroeder et al., 2008). The combustion equilibrium calculations obtained from the properties of the reactant species and of equilibrated adiabatic products using the species and their thermodynamic values from the different data files. GASEQs chemical equilibrium models assumes adiabatic conditions in constant volume, and formation of equilibrium-defined concentrations of post explosion compounds and their expansion due to the temperature rise caused by the liberated heat assuming ideal gas behavior. This approach represents ideal deflagrations in closed systems well and gives the highest possible attainable explosion pressures. The present numerical method allows the determination of the most conservative values of Pad, and may be used as suitable for prediction of experimental data. Thus, at the first stage, the equilibrium calculations can be used as a rough calculation of a worst case scenario. At the same time, these values have been used as approximate initial values for explosion experiments carried out in heated 1 m3 explosion apparatus built by OZM Research s.r.o. at Energy Research Centre, VŠB - Technical University of Ostrava.
Dimensionless experimental formulae
Simple dimensionless experimental formulae equation (1) based on polynomial functions are proposed for correlation of the pad of CH4/N2/O2 and H2/O2/N2.
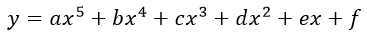 (1)
(1)
where a, b, c, d, e and f are the constants in the scientific notation with a precision of E-04; y is the pressure; x is the mole fraction of the fuel.
The formulae are based on data obtained from theoretical predictions and carried out at fixed atmospheric conditions. The proposed approach requires only five coefficients and mole fraction of components to be known in advance. These 5 coefficients inherently affected by the uncertainty in the experiments and the regression procedure. According to the results, the pressure has been approximated by a polynomial approximation of the fifth degree. The polynomial approximation has been realized with Excel by the utilization of a scatter graph. Experimental data were used for formulae verification and validation obtained results indicate that accuracy is comparable and to some extent better than that of conventional thermodynamic prediction models. Data correlations by equation (1) for CH4/N2/O2 and H2/O2/N2 mixtures were performed together with iterative calculations.
Experiment
Measurements of the maximum explosion pressure parameter, Pmax, has been performed in the 1 m3 explosion chamber (OZM Research s.r.o., Czech Republic) described in Figure 1 and further described in (Skřínský et al., 2016).

Fig. 1: General diagram of the testing system adopted for the CH4/O2/N2 tests
The explosion chamber allows the measurement of gas explosion parameters in accordance with the terms and specifications in EN 1839. High purity gases (H2: 99.995%, CH4: 99.995%, O2: 99.95%, N2: 99.9995%) have been used to prepare the mixtures, relying on the partial pressures method. The gasses have been dosed into the chamber from the dosing vessel equipped by three inputs for connection to cylinders with nitrogen and oxygen and line for free suction of air from outside. The ignition source is located in the geometrical centre of the cylinder. In the experiment, ignition was performed with stainless steel electrodes. After vacuum, the combustion vessel was filled by injecting one mixture component. The material and components comply with the use of equipment for experiments at atmospheric initial pressure and initial laboratory temperature (15-30 °C). The explosion chamber is equipped with measurement of time depended dynamic pressure using two pressure sensors (Kistler type 701A, accuracy: 0.00125 MPa, sampling rate: 400 000 samples/s) and also by the measurement of the flash duration. Pressure range is up to 25 MPa calibrated for the range up to 2.5 MPa. The test method is designed to produce measurement of the explosion pressure and the maximum explosion pressure of a quiescent flammable gas/air/inert mixture in an empty closed volume at ambient temperature and pressure.
Analysis
The aim of the analysis is to identify the differences between 4 thermodynamic databases (thermdat.tdd, Burcat.tdd, Leeds.tdd, Thermo.tdd) written in CHEMKIN format of thermodynamic database (14 coefficients) or if using Burcat's thermodynamic database (15 coefficients). The comparison based mainly on the values of the products specific heat (Cp), the enthalpy (H0) and the entropy (S0) of a species at any given temperature (298.15 K) and on the value of adiabatic flame temperature, T. The results of comparison for 5 equilibrated adiabatic products (N2, H2O, CO2, CO, O2) are in Figure 2.
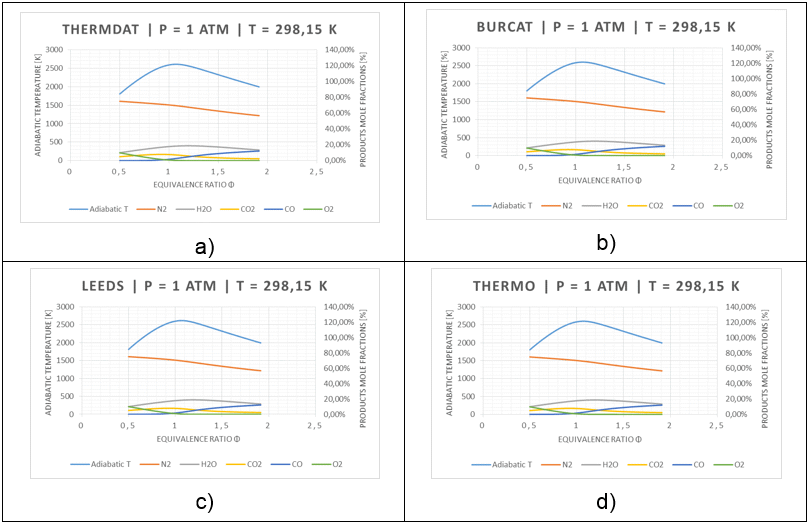
Fig. 2: General diagram of the testing system adopted for the CH4/O2/N2 tests
In Figure 2a-d the calculated equilibrium compositions and the flame temperature of the combustion product have been plotted against equivalence ratio. We can see directly that the results are very close. For all graphs in Figure 2, the adiabatic flame temperature reaches a peak very close to the stoichiometric condition (where equivalence ratio Φ=1) on the slightly fuel-rich side (where equivalence ratio Φ>1). Because the system is slightly under-oxidized, the specific heat of the product is reduced and therefore the flame temperature is increased. Dissociation of combustion products also contributes to this shifting effect (Kenneth and Kuo, 2005).
Results and discussions
Fig. 3 reports the calculated adiabatic pressure and maximum adiabatic pressure and Table 2 the calculated polynomial approximation of adiabatic explosion pressure, Ppol. To enable a comparison with results of Pmax and Pad were determined as illustrated by Figure 3. The adiabatic pressure as calculated by described computational approaches is shown, for the sake of adiabaticity rather than validation.
Thermodynamic model
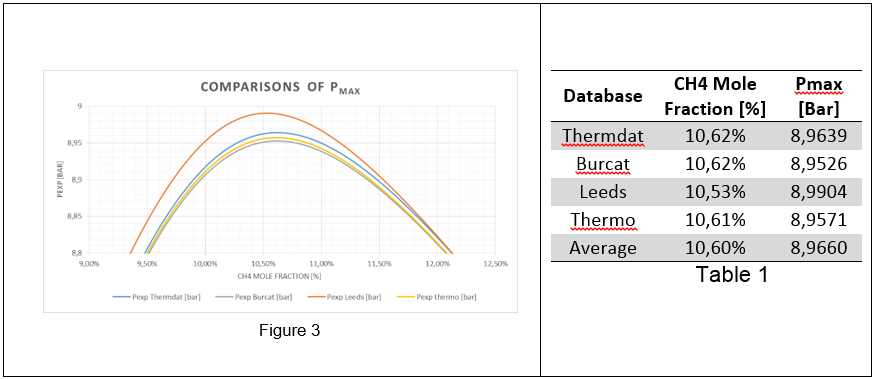
Fig 3: Maximum adiabatic pressures calculated for CH4/N2/O2
Fig 4: Maximum adiabatic pressures calculated H2/O2/N2
In Figure 3-4 the maximum adiabatic pressures calculated are, as expected; lower than theoretical (see Table 1, Pmax) due to non-adiabaticity of the combustion in chamber, however confirming the thermodynamic trend. The values of Pad are consistent with the maximum difference in the order of 10-2 bar(a). The average value from 4 thermodynamic databases has been used for further comparison.
Dimensionless experimental formulae for CH4/N2/O2and H2/O2/N2
Table 2 describes the flashpoint approximations and predictions for CH4/N2/O2 and compares them with the root mean square from the least square analysis.

Table 2: Dimensionless experimental formulae for CH4/N2/O2 Pad

Table 3: Dimensionless experimental formulae for H2/N2/O2 Pad
It can be seen that the predictive values for the flashpoint simulation are almost identical to the than the corresponding Pad, and somewhat larger than experimental derived data for both CH4/N2/O2 and H2/O2/N2 molecular systems. This approach represents ideal deflagrations in closed systems well and gives the highest possible attainable explosion pressures. The present numerical method allows the determination of the most conservative values of Pad and could be used as a rough estimate of explosion pressure in safety engineering applications.
Summary
Table 4 give the results on Pmax, Pad, Ppol for CH4/O2/N2 and H2/O2/N2 mixtures compositions adopted in the gas explosion experimental studies.
| Test | Fuel | Air | Pad | Ppol | Pmax | Pad- Pmax | Pad-Ppol |
|---|---|---|---|---|---|---|---|
| (-) | (vol.%) | (vol.%) | (bar) | (bar) | (bar) | (bar) | (bar) |
| CH4 | 10.5 | 89.5 | 8.97 | 8,92 | 8.42 | 0.55 | 0.05 |
| H2 | 32.0 | 71.0 | 8.08 | 8.08 | 8.01 | 0.90 | 0.00 |
Conclusion
The explosion behavior of stoichiometric CH4/O2/N2 and H2/O2/N2 mixtures at atmospheric conditions has been studied both experimentally and theoretically at different fuel concentration. Explosion tests were performed in a 1m3 closed cylindrical vessels at standard atmospheric conditions. Measured pressure time trends have been evaluated and the maximum peak pressure calculated as a mean value from two pressure sensors. All tests show the typical trends in closed combustion chamber. Computed adiabatic temperatures, post-combustion products concentrations, and maximum explosion pressures for methane-air mixtures (4.80 vol. %, 10.50 vol. %, 15.50 vol. %) at ambient temperature and ambient initial pressure are presented. The adiabatic maximum pressure calculated are, as expected; lower than experimental value due to non-adiabaticity of the combustion chamber, however confirming the thermodynamic trend. The suggested approximation provides accuracy comparable and to some extent better than that of the thermodynamic methods.
Acknowledgement
This work was prepared within the project „Innovation for Efficiency and Environment – Growth“, identification code LO1403 with the financial support from the Ministry of Education, Youth and Sports in the framework of the National Sustainability Programme I.
References
[1] SCHROEDER, V. …[et al.]. 2008. Chemically unstable gases: Flammability of ethylene oxide mixtures in sterilization processes. In 42nd Loss Prevention Symposium, LPS 2008, Topical Conference at the 2008 AIChE Spring National Meeting, 2008. S. 489-496.
[2] LEES, F. P. 2012. Loss Prevention in the Process Industries: Hazard Identification, Assessment, and Controls: Volume 1-3. Oxford: Butterworth-Heinemann, 2012.
[3] CROWL, D. A.; LOUVAR, J. F. 2002. Chemical Process Safety: Fundamentals with Applications. 3rd Ed.. Prentice Hall, 2002. (International Series in the Physical and Chemical Engineering Sciences). ISBN 978-0131382268.
[4] ECKHOFF, R. 2005. Explosion Hazards in the Process Industries. 1st ed. Gulf Publishing Company, 2005. 436 s. ISBN 978-0-9765-1134-2.
[5] GASEQ, A. Chemical Equilibrium Program for Windows. Available at: http://www.c.morley.dsl.pipex.com/.
[6] KUO, Kenneth K. 2005. Principles of combustion. 2nd ed. Hoboken: John Wiley and Sons, 2005. 760 s. ISBN 978-0471046899.
Vzorová citace
MAHIN, Jérôme; SKŘÍNSKÝ, Jan. Determination of explosion characteristics of fuels/air mixtures: polymonial approximations. Časopis výzkumu a aplikací v profesionální bezpečnosti [online], 2016, roč. 9, č. 1-2. Dostupný z: http://www.bozpinfo.cz/josra/josra-01-02-2016/determination-explosion-charac.html. ISSN 1803-3687.
Užitečné odkazy
Provozovatel portálu
Jeruzalémská 1283/9
110 00 Praha 1


